In the field of engineering and natural sciences, measuring instruments usually do not permit the precise determination of the exact values of the measured quantities. We have to be satisfied with approximate values. We are often compelled to work with approximations since the exact values are frequently indeterminate.
When measuring, we encounter two values, which are marked differently. Namely:
approximate value of the measured quantity, denoted by A
exact value of the measured quantity, denoted by a
According to the type of error, we distinguish two errors:
By absolute error, we express the absolute limits within which the true value of the measured quantity probably lies. So:
With an absolute error, we express the size of the error we made:
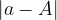
Also valid if 
denotes the maximum possible value for the absolute error, then the exact value is limited by
but written differently
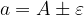
This notation is understood to mean that a is at most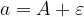 
and at least 
.
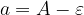Note: is the Greek letter epsilon.
When calculating with approximations, the absolute rule is:
Let a and b be the exact values of the measured quantity and let A and B be the corresponding approximations.
Then the absolute error of the sum (difference) is less than or equal to the sum of the absolute errors of the sums:
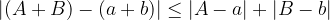
Often, when estimating errors, we are more interested in its relationship to the exact value than the size of the error. The resulting ratio is called the relative error. So:
The relative error expresses the accuracy of the measurement and is equal to:
The relative error is usually expressed as a percentage and marked with the letter * *r* *.
When calculating with approximations, the following rules apply to relative error:
Let a and b be the exact values of the measured quantity and let A and B be the corresponding approximations. Then the following applies:
The relative error of the product is less than or equal to the sum of the relative errors of the factors:
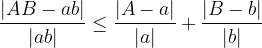
Relative quotient error is the sum of the relative errors of the numerator and denominator
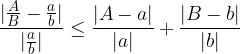
Rounding off is used when we do not need completely accurate results. Approximations are made with each rounding. For each subsequent approximation, the error is greater than or equal to.
The following rule applies:
if the first digit of reference digits is 0,1,2,3 or 4, the retained digits remain unchanged
if the first digit after the referenced digit is 5,6,7,8 or 9, the last retained digit is incremented by 1
Note: If the last digit retained is 9, the previous digit must also be incremented by 1.
We distinguish two types of rounding:
Rounding to n-digit / significant figures:
A number is written in n-places exactly if it has n - digits in its notation, and zeros before the first non-zero digit are not counted.
Rounding to n-decimals exactly:
A number is written to n-decimals exactly if it has n - digits in its notation after the decimal point. In this case, all zeros are also considered as a decimal point, regardless of whether they are preceded by a non-zero digit.
Note: when adding, subtracting, dividing and multiplying, we usually round the result to as many decimal places as the factor with the least decimal places.
