The absolute value of a real number in mathematics is an elementary function that represents its distance from the numerical origin (point 0) on the number line.
The absolute value of the number a is usually indicated by a vertical bracket: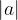 
We know that the distance from the coordinate origin is never negative, so the absolute value of any number is always a non-negative number.
The absolute value is therefore:
the absolute value of a positive number is equal to the given number,
the absolute value of a negative number is equal to the additive inverse of the given number,
the absolute value of number 0 is equal to 0
Mathematically, this can be written as:
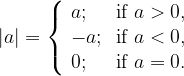
Let a and b be arbitrary real numbers. Then the following rules apply:
is valid exactly when
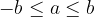
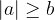applies exactly when
and
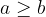
Absolute value has the following properties in real space:
The absolute value of the number a is positive or equal to 0:
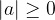
The absolute value is equal to 0 exactly when a = 0:
Points a and - a are equidistant from the coordinate origin, so their absolute value is the same. Equality follows directly from the definition of absolute value:
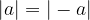
The absolute value of the product is equal to the product of the absolute values:
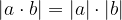
The absolute value of the quotient is equal to the quotient of the absolute values.
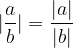
The absolute value of the sum is less than or equal to the sum of the absolute values. This property is called triangular inequality:
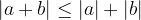
Consequently, the following also applies:
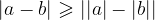
Absolute value has two important meanings in geometry:
Point distance a:
On the number line, | a | is the distance of the point a from the origin of the coordinate system.
Graphically, this is shown as:
and
Distance between points a and b:
Using the absolute value, we can calculate the distance between the points a and b. The peculiarity of the absolute value is that we do not need to first determine which number is greater than the other (we know: the absolute value of any number is always a non-negative number.) So:
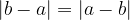
Mathematically, we write this as:
The distance between the points a and b is the same:
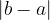
Graphically, this is shown as:
