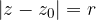The absolute value of the complex number z = a + bi is:
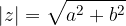
It can also be calculated according to the form:
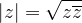
The absolute value of a complex number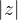 
geometrically represents the distance of a complex number z (the point it represents) from the coordinate origin:
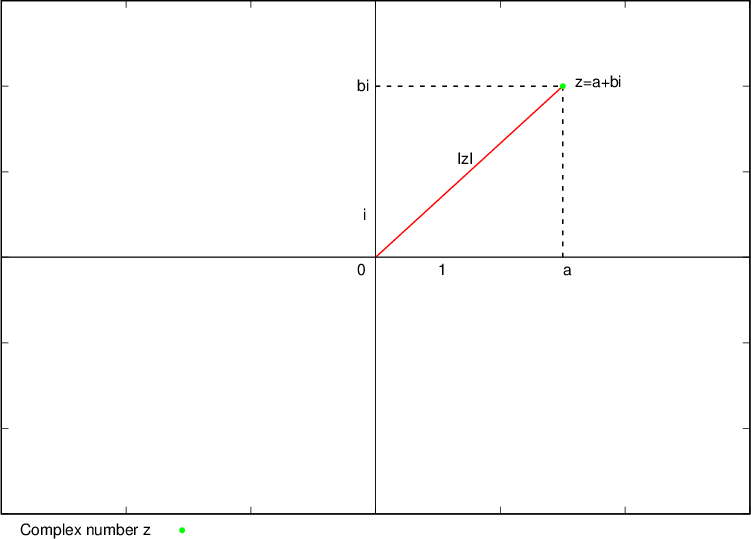
The following laws apply to the absolute values of complex numbers:
The absolute value is a non-negative real number:
The absolute value of a complex number is zero if and only if the complex number is equal to 0:
The complex number z, its additive inverse and its conjugate, all have the same absolute values:
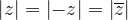
The conjugate value of the product of two complex numbers is equal to the product of their conjugate values:
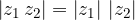
The absolute value of the sum of two complex numbers is less than or equal to the sum of their absolute values:
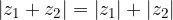
A circle in a complex plane with centre at the point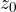 
and radius r is defined by the equation:
