

A voltage can be direct or indirect.
Several forms of alternating voltage are used. In computing, it has the shape of rectangular pulses, in video technology, it has a sawtooth shape, and in energy networks, it has a sinusoidal shape. Various forms of AC voltages for circuit testing can be generated using a function generator. We observe them with the help of an oscilloscope. The oscilloscope shows us a graph of voltage (y-axis) against time (x-axis) - see the image below.
In the following, we will limit ourselves to a sinusoidal voltage. In this case, the voltage varies according to a sine curve. It is determined by the maximum value or amplitude and frequency.
Obtaining sinusoidal alternating voltage for energy purposes is most often done with the help of alternating voltage generators. These convert mechanical energy into electrical energy.
Let's imagine that a coil with windings rotates in a homogeneous field, as shown in the figure.
The magnetic flux through the loop is given as:
Due to the change in the magnetic flux, according to Faraday's law of induction, a voltage is induced in the coil which is given as:
The equation for sinusoidal alternating voltage is given as:

where 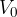 is the maximum value or amplitude and is given as:
is the maximum value or amplitude and is given as:
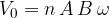
If we connect an AC voltage to a load resistor of resistance 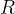 , it has an electrical power
, it has an electrical power 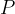 which is given as:
which is given as:
The electrical power therefore changes with time between zero and maximum power, as shown in the figure below:
The average power 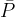 , with the help of which we also calculate the electrical work, is obtained by equating the area under the AC power graph (gray hatched) to the area under the average power graph (green lines). We get:
, with the help of which we also calculate the electrical work, is obtained by equating the area under the AC power graph (gray hatched) to the area under the average power graph (green lines). We get:
The root-mean-square (rms) or effective voltage 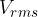 is the direct voltage that would give the consumer the same power as the alternating voltage with a maximum value of
is the direct voltage that would give the consumer the same power as the alternating voltage with a maximum value of 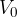 and for a sinusoidal alternating voltage, it is given as:
and for a sinusoidal alternating voltage, it is given as:
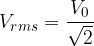
If it is written in the data that the mains voltage is 230 V, this means its effective (and not maximum) value.
With the help of effective voltage, we can directly (without conversion) calculate electrical power and work.
The effective voltage is often written without an index, that is, only 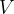 . The same applies to the average power, it is written only with
. The same applies to the average power, it is written only with 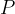 .
.
The mains voltage in the household is e.g. 230 V (this is the rms/effective value) and a frequency of 50 Hz.