From the theory of linear function we recall that the slope angle of a line is determined by the gradient m, which is equal to the differential quotient:
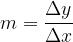
By definition, the tangent of the angle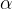 
is:
from the sketch below we understand that this ratio is the same as:
We can conclude:
The gradient of a line is equal to the tangent of the angle 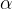, which the line encloses with the x axis.
To calculate the angle between two lines, let's have a sketch:
We know that the sum of the interior angles in a triangle is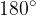 
.
To calculate the acute angle between two lines, we use the absolute value of the expression:
Formula for calculating the acute angle between two lines:
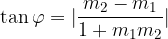
From the equation we can quickly determine:
Parallelism of two lines
We know that lines are parallel when they have the same gradient:
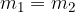
It follows from the equation that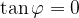 
or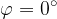 
. Which is the result we expected for two parallel lines.
Perpendicularity of two lines
Two lines are perpendicular when the gradients are:
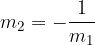
It follows from the equation that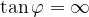 
, which is true when 
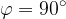. Which is the result we expected for two perpendicular lines.
