A quadrilateral is orthodiagonal if its diagonals intersect at right angles. The area of any orthodiagonal quadrilateral with diagonal e and f is given as 
.
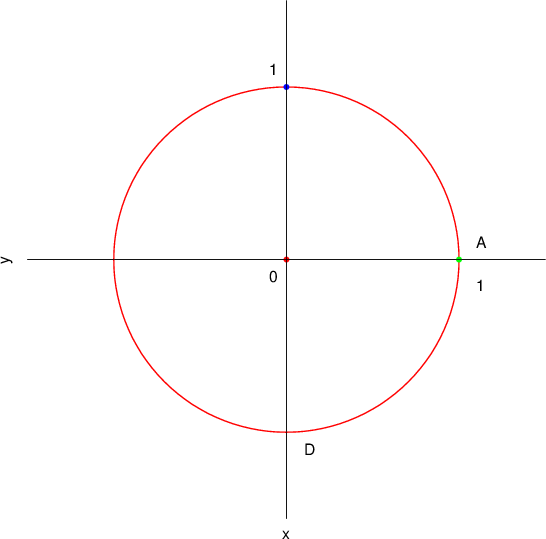
Let 
be such points on the unit circle that the quadrilateral ABCD is a trapezium with bases AB and CD. The diagonals of the trapezium intersect at the point P.
Let O be the origin of the coordinate system and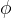 
be the size of the angle AOB.
Prove that trapezium ABCD is isosceles. Draw a sketch.
Calculate the sizes of the angles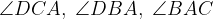 
and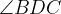 
and prove that the trapezium ABCD is orthodiagonal.
Express the coordinates of the point B and the length of the diagonal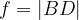 
in term of .
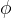Express the area of the trapezium ABCD in term of 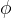. Which point B on the unit circle will give the maximum area of the trapezium ABCD? Justify your answer.
.
