Personal collections


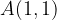 ,
, 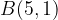 and
and 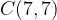 are given in a plane. By mirroring the point B over the line
are given in a plane. By mirroring the point B over the line 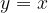 , the point D is gotten.
, the point D is gotten.Draw the points A, B, C and D in the coordinate system below and obtain the equation of the triangle of the outlined circle.
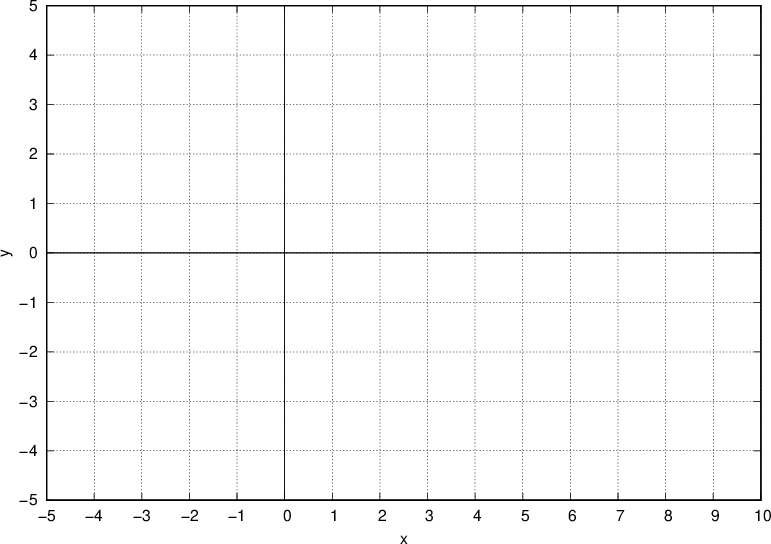
Calculate the area of quadrilateral ABCD
Rotate the triangle ABC by  around the side AC to get the geometric shape G. Prove that the volume of the solid G is
around the side AC to get the geometric shape G. Prove that the volume of the solid G is 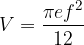 , where
, where 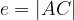 and
and 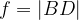 .
.
Calculate the abscissa of the point T on the x-axis so that the sum of the squares of the distances from the point T to the point A and from the point T to the point C is minimal.