Within the differential quotient limit, the change in the independent variable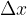 
is infinitesimal. Label it with 
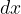. The change in the function value 
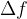is also correspondingly small due to the continuity of the function f. Label it with 
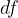. So we get derivative:
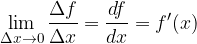
from which we derive:
The differential of the function df is derived from the above equation or from the derivative:
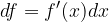
The differential of the function f is denoted by 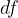and is the same
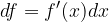
The differential of the function tells us by how much the ordinate changes when changing the abscissa dx on the tangent at the point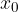 
(and not on the graph of the function!). For a small change in x, the differential of the function on the tangent is almost equal to the change in the ordinate of the function and can be taken as a good approximation of the change in the function.
To make it easier to understand, let's show this graphically:
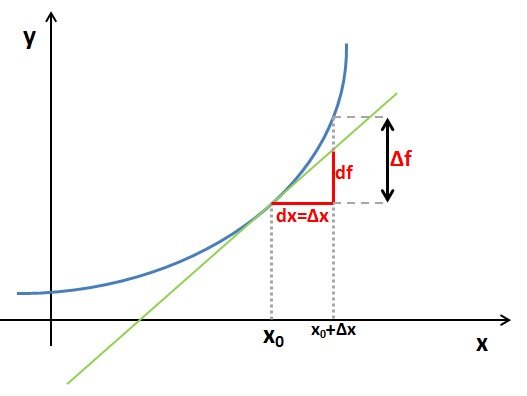
Differential df on the tangent, for a small variable dx is almost the same as the change of the function 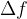, so we can write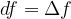 
The differential is also often used in the approximate calculation of functional values. We usually do this when calculating the true functional value is too complicated.
We calculate the approximate functional value by the formula:
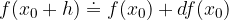
or, we write the differential as:
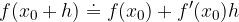
Using the derivative, we derive a formula for calculating approximate functional values:
So if we look for the value of the function f at the point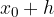 
, but we know the functional value at the point 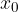, we add the differential of the function to it and get the approximate value of 
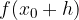. Instead of the real increment of the function, we added the differential, which means the increment of the linear function - the tangent to the curve. Let's look graphically:
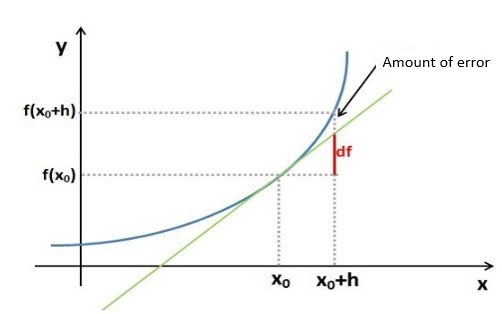
The graph clearly indicates the error we make when using the equation to calculate the approximate value of the function.
