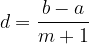A sequence is arithmetic if the difference between two consecutive terms is constant or when each subsequent term of the sequence is calculated by adding the same number to the previous one.
We write some consecutive terms of the arithmetic sequence, denoting the difference of two consecutive terms by d, and the first term of the sequence by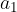 
.
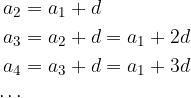
We write the form for the general term of the arithmetic sequence:
The form for the general arithmetic sequence term, where 
, is:
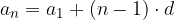
The general term of an arithmetic sequence is considered to be a linear function of the variable n.
The difference of two consecutive terms is called common difference, denoted by d. The difference is always constant.
The form for arithmetic sequence difference, where is:
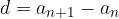
or
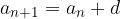
An Increasing / decreasing arithmetic sequence depends on the common difference of the sequence as follows:
if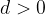 
, then the sequence is increasing
if is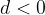 
, then the sequence is decreasing
if is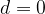 
, then the sequence is constant
Each term of the arithmetic sequence, with the exception of the first, is equal to the arithmetic mean of its neighbors.
Arithmetic mean of any two numbers a and b is the number:
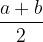
The arithmetic mean of two arbitrarily symmetrically lying terms of a sequence is the term:
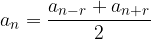
Let us have the numbers a and b and say that we want to insert m numbers between these two numbers so that the numbers 
form an arithmetic sequence. This process is called linear interpolation.
By linear interpolation we obtain an arithmetic sequence which is considered to consist of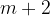 
terms, the first term 
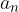is equal to a and the last term 
is equal to b.
Let's find the form for calculating the common difference of the arithmetic sequence thus obtained:
The form for the common difference, obtained by linear interpolation when m numbers are inserted between the numbers a and b, is:
