Personal collections


A capacitor is an electrical element that can store charge. The simplest capacitor consists of two parallel metal plates of area 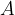 , which are separated by distance
, which are separated by distance  . If there is air between the plates, it is an air capacitor. We can also add a substance (dielectric) between the plates and thereby increase its capacitance, stability, etc. (see Figure 1).
. If there is air between the plates, it is an air capacitor. We can also add a substance (dielectric) between the plates and thereby increase its capacitance, stability, etc. (see Figure 1).
If a voltage is applied across the capacitor, it receives a charge. The charge remains in the capacitor even if the voltage source is removed. It can be discharged if a consumer (load) is connected to it: e.g. bulb or resistor. In this, it is similar to a battery or accumulator.
The stored charge in the capacitor is usually too small for energy purposes compared to the battery. It is sufficient, for example, for the current illumination of an object being photographed (camera flash).
The capacitor is used primarily in electronics. It has the property of transmitting alternating current, and the more so, the higher its frequency. It does not transmit direct current.
Let's take two parallel metal plates with an area 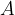 and let the distance between the plates be
and let the distance between the plates be  . Between the plates can be air or a dielectric with a relative dielectric constant of
. Between the plates can be air or a dielectric with a relative dielectric constant of 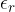 . The device is called a capacitor.
. The device is called a capacitor.
If we connect a voltage  across the plate, the plates receive a charge
across the plate, the plates receive a charge 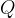 which is given as:
which is given as:
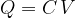
The notation 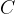 is called the capacitance of the capacitor. The unit of capacitance is
is called the capacitance of the capacitor. The unit of capacitance is 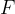 (Farad).
(Farad).
But, what is  ?
?
Let's answer this question by making 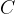 the subject of the formula above:
the subject of the formula above:

Let's replace the quantities with their units. So Farad is:
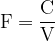
A capacitor has a capacitance of 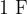 (farad) if it receives a charge of
(farad) if it receives a charge of 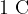 at a voltage of
at a voltage of 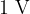 .
.
Let's derive the equation for the capacitance of a capacitor consisting of two parallel plates according to Figure 1. We take into account that the electric field between the plates is homogeneous, i.e., the same magnitude and the same direction in all points of the space inside the plates. This is true if the two plates are large enough and the distance between them is small enough.
Let's write the formula for 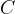 :
:
Here, the constant, permittivity of free space 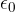 is given as :
is given as :
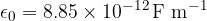
The constant, relative permittivity 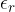 of the dielectric is unitless and depends on the substance (dielectric) between the capacitor plates. If there is air between the plates:
of the dielectric is unitless and depends on the substance (dielectric) between the capacitor plates. If there is air between the plates:

We have obtained the formula for the capacitance of a capacitor. It depends on the material (dielectric) and geometry: the size of the plates and the distance between them. Let's confirm the unit of capacitance using the new formula above:
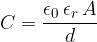
Let's insert the units of the quantities in the fraction on the right-hand side of the equation to obtain 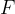 :
:
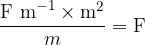
A capacitor is a device, an element in electrical engineering, designed to store an electric charge.
Capacitance 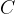 is the body's ability to receive a charge
is the body's ability to receive a charge 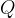 if a voltage
if a voltage  is applied across it.
is applied across it.
This is expressed mathematically as:
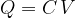
It is essentially a geometric property. It depends on the area of the plates, the distance between the plates, and the material of the dielectric.
The capacitance of a capacitor is calculated using the formula:
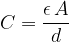
where:
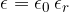
where 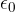 is the permittivity of free space and
is the permittivity of free space and 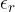 is the relative permittivity of the dielectric (in the case of air, it is 1).
is the relative permittivity of the dielectric (in the case of air, it is 1).
The unit of capacitance is 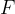 (farad). A capacitor has a capacitance of
(farad). A capacitor has a capacitance of 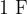 (farad) if it receives a charge of
(farad) if it receives a charge of 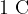 at a voltage of
at a voltage of 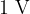 .
.
When several capacitors are connected in series, the charge on all capacitors is the same. The first plate of the first capacitor receives a charge of 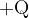 . The charge exerts an attractive force on the electrons on the opposite plate(s). Since this one is connected to the next capacitor with a conductor, its first plate is charged to
. The charge exerts an attractive force on the electrons on the opposite plate(s). Since this one is connected to the next capacitor with a conductor, its first plate is charged to 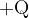 , since the total charge must be equal to zero (as much as there are more electrons on one side - i.e. negative charge, there must be fewer electrons on the other side - positive charge).
, since the total charge must be equal to zero (as much as there are more electrons on one side - i.e. negative charge, there must be fewer electrons on the other side - positive charge).
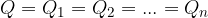
The voltage  is distributed across the capacitors such that:
is distributed across the capacitors such that:

Let's note that:
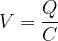
Therefore:
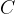 is called the total or combined capacitance. It can also be called the replacement capacitance as it is the capacitance of the capacitor that would replace the series connection of the capacitors.
is called the total or combined capacitance. It can also be called the replacement capacitance as it is the capacitance of the capacitor that would replace the series connection of the capacitors.
When capacitors are connected in series, the charge on all capacitors is the same. The voltage is distributed across the capacitors in inverse proportion to the capacitance. The reciprocal value of the total capacitance of all the capacitors is the sum of the reciprocal values of the capacitance of the individual capacitors:
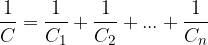
When connected in parallel, all capacitors have the same voltage. The total charge is equal to the sum of the charges on the capacitors.
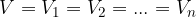

Let's note that:
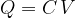
Therefore:
When capacitors are connected in parallel, the voltage across all capacitors is the same. The charge is distributed across the capacitors in proportion to their capacitance. The total capacitance of the capacitors is the sum of the capacitances of all the capacitors:
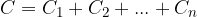
As we increase the voltage, the capacitor is charged so that the charge increases linearly with the increasing voltage.
The energy of the capacitor is equal to the area under the graph of the charge 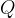 against the voltage
against the voltage  :
:

Substituting the equations 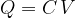 and
and 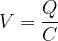 into the equation above, we obtain the equation in two different forms below:
into the equation above, we obtain the equation in two different forms below:
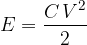
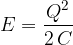
The energy of the capacitor is contained in the electric field, which we will show below.
Let's write the formula of the energy again:
The energy of the capacitor is therefore in the electric field  , which is covered by the volume
, which is covered by the volume  between the plates.
between the plates.
The energy of a capacitor is calculated using one of the formulas below:
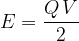
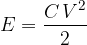
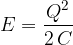
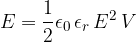
From the last formula, we conclude that the energy of the capacitor is stored in an electric field  .
.