Personal collections


Understanding the coordinate system is the basis for any graph drawing. There can be several coordinate systems, but for us at this moment the rectangular coordinate system will be important.
The rectangular coordinate system is also called the Cartesian coordinate system; it was named after the famous mathematician Rene Descartes (1596-1650), who was the first to really take advantage of the usefulness of such a coordinate system.
A rectangular coordinate system in a plane consists of two number lines that intersect at the point 0 (the origin). The horizontal line is called the abscissa axis, denoted by x, and the vertical line is called the ordinate axis, denoted by y.
A point in the coordinate system is determined by two real numbers, which we call the coordinate points T (x, y). These two numbers tell us where the point lies in the coordinate system. The first value belongs to the abscissa axis and the second to the ordinate axis.
The coordinate system is divided into four quadrants:
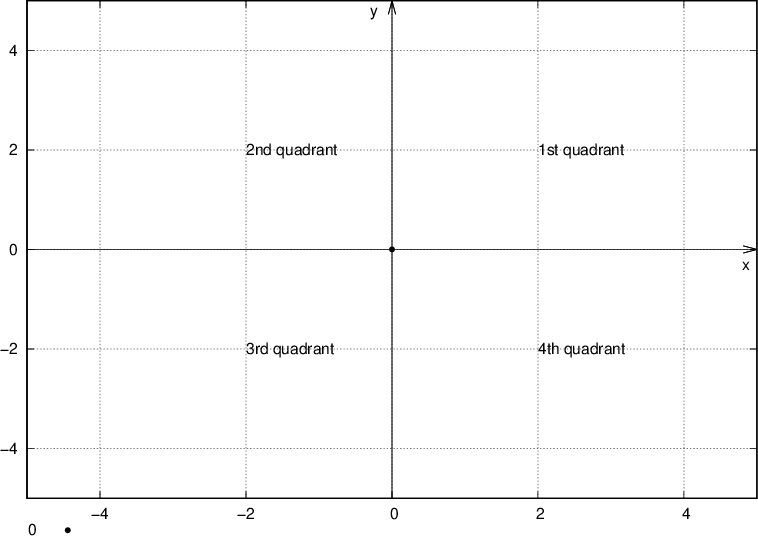
From the graph we can understand that we:
have a positive abscissa and ordinate in the first quadrant of the point
have in the second quadrant of the point a negative abscissa and a positive ordinate
have a negative abscissa and a negative ordinate in the third quadrant
have in the fourth quadrant a positive abscissa and a negative ordinate
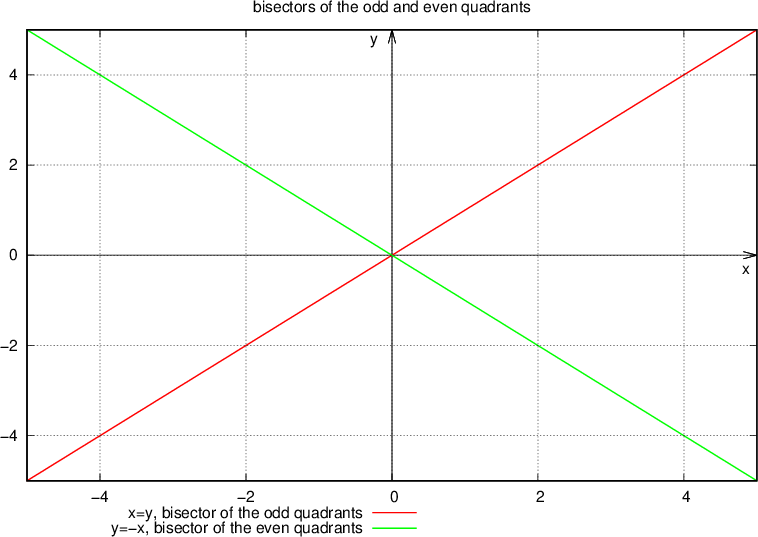
We have two bisectors of the quadrants:
the odd quadrant bisector determined by the linear equation y = x,
the even bisector of the quadrants determined by the linear equation y = - x.
Mirroring is a common name for a basic geometric mapping. Each mirroring maintains the distances between the points, so it is classified as a rigid movement. The name mirroring derives from the fact that mirroring a given geometric set gives a similar result as reflecting light on a mirror.
When mirroring, there are always two concepts:
The point or set of points or function to be mirrored.
The point or function through which it is mirrored.
Below we will look at the basic mirrors. We will mirror the point via the coordinate axes or via the coordinate origin.
A point in the rectangular coordinates is mirrored by the system over the abscissa axis by drawing a mirror point over the abscissa axis. In doing so, it retains the properties of the point being mirrored, i.e it is equidistant from the abscissa and the ordinate axis, except that its sign changes in the ordinate axis.
Mirroring over the abscissa is written as

A point in the rectangular coordinates of the system is mirrored over the ordinate axis by drawing a mirror point over the ordinate axis. In doing so, it retains the properties of the point we are mirroring, i.e it is equidistant from the abscissa and the ordinal axis, except that its sign changes at the abscissa axis.
Mirroring across the ordinate axis is written as

A point in the rectangular coordinates is mirrored by the system over the coordinate origin by drawing a mirror point over the origin. In doing so, it retains the properties of the point we are mirroring, i.e it is equidistant from the abscissa and the ordinate axis, and its sign changes at both coordinates.
Mirroring over the starting point is written as
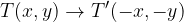
Now that we know how to draw a point in a rectangular coordinate system, we will look at some examples of how to draw a monoset of points in a plane. Let’s look at some basic examples.