If we want to determine the position of any point, we need to know the cartesian coordinate system. The cartesian coordinate system we will use depends on where the point is located in either a plane or space.
In this chapter, we will focus on points in space. To determine their position, we need to know the cartesian coordinate system in space, which is drawn according to the following procedure:
We select any point in the space and mark it with 0. The point 0 is called the coordinate origin:
Now we draw three lines where a line is perpendicular to the other two:
The lines conform to the system of the right-handed rule, as shown in the figure:
We choose a unit to obtain number axes, which we call coordinate axes:
The coordinate axes are named. The first two are already known from the coordinate system in plane, i.e the x-axis and the y-axis. The third is the z-axis.
The position of the point T with respect to the chosen coordinate system is written with three coordinates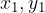 
and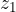 
, where 
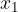is the first coordinate of point T and tells us the section on x axis, 
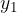the second coordinate of point T and tells us the section on y axis and 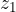, the third coordinate of point T and tells us the section on z axis.
The position of point T, which is written as an ordered triple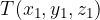 
, is thus precisely defined and is not the same as 
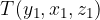. If we change the order of the coordinates within the ordered triple, we get different points.
Let's look at an example of a point and a set of points in space:
