We describe the circle with centre (point C) and radius (distance r) or diameter (distance d, which is twice the radius). The centre determines the position of the circle in the plane, and the radius its size.
Circle is a self-contained curve that is exactly one radius away from the centre at each point:
If we add the space bounded by the curved surface of the circle, we get the area:
Let’s not forget that the circle also contains other circles.
Let's define the terms discussed so far:
A circle is a two-dimensional shape bounded by a curved surface called circumference where every point on the circumference is the same distance from the centre.
Centre is a point located in the middle of the circle and equidistant from all points on the circle. Let's mark it with a capital letter C.
Radius is the distance from the centre to any point on the circle. Let it be marked with a small capital letter r.
Diameter is the maximum distance between two points on a circle. Let's mark it with a small letter d.
The formula for the circumference of a circle is:
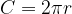
The formula for the area of a circle is:
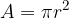
Let l be an arc with points at points A and B, k be the complementary arc of the arc l.
The central angle above the arc l has a vertex in the centre of the circle, and its sides intersect the circle at the ends of the arc.
The inscribed angle above the arc l has a vertex at point C on the arc k, and its sides intersect the circle at the edges of the arc:
Inscribed angle theorem reads:
The central angle measures twice the value of the circumferential angle above the same arc:
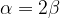
Let line AB be the diameter of the circle. The arc AB and its complementary arc represent semicircles.
If the vertex of the angle 
lies on a semicircle and the sides run through the diameters of the diameter, then 
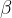is the right angle.
An arc is the part of a circle bounded by two points.
Arcs with the same ends are called complementary arcs.
The complementary arcs together make up the entire circle (marked l and k in the figure):
An arc whose edges are equal to the edges of the diameter is called a semicircle.
The ratio of the length of the circular arc and the total circumference of the circle is equal to the ratio of the size of the central angle and full angle:
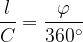
Taking into account the formula for the circumference of the circle, we can thus write:
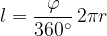
Chord is a line that connects two points on a circle. The longest chord is the diameter.
Chords with ends A and B
Sector is a set of points bounded by an arc and two radii to the edges of the arc.
The ratio of the area of the sector and the area of the whole circle is equal to the ratio of the size of the central angle and full angle:
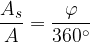
Taking into account the formula for the area of a circle, we can thus write:
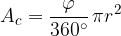
Segemnt is the set of points bounded by an arc and a chord between the ends of the arc.
The area of a segment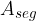 
is obtained by reducing the area of a sector above the central angle 
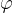by the area of an isosceles triangle ABS (see figure above), whose sides are equal to the radius of the circle, and its base is chord between the ends of the arc above the central angle :
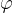Taking into account the formula for the area of a sector and the area of an isosceles triangle, we can thus write:
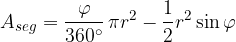
The above formula holds on the assumption that the central angle is less than 180 °:
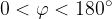
The derivation of the equation for the area of an isosceles triangle ABS can be seen in the chapter The right n-angle.
A circular ring is a set of points between two circles with a common centre and different radii.
The radii are marked in the figure with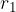 
and 
:
The area of a circular ring is obtained by subtracting the area of the smaller (inner) circle from the area of the larger circle:
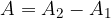
Taking into account the formula for the area of a circle, we can thus write:
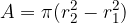
A straight line can intersect, touch, or run through a circle:
Secant is a line that intersects a circle at two points. Secant is a chord carrier.
A tangent is a line that touches a circle at exactly one point. The tangent is perpendicular to the radius.
Parallel is a line that has nothing in common with a circle.
Secant s, tangent t and parallel m
We can draw a circle on the triangle (circumscribe). We use the line bisector. Each side of a triangle is a line and we can draw a bisector. The line bisector is characterized by the fact that each point on it is equidistant from both ends of the line, in our case these are the two vertices of the triangle. If we want to draw a circle on a triangle, we need to find a point that will be equidistant from all three vertices of the triangle. To do this, we draw a bisector on each side of the triangle:
Circumscribed circle
The point where the bisectors of the sides intersect represents the centre of the triangle. The vertices of a triangle are exactly half a radius away from this point, so a circle can be drawn through them.
We can also draw a circle (inscribe) in a triangle. We use the angle bisector. The triangle has three angles and we can draw a bisector to each of them. An angle bisector is characterized by the fact that each point on it is equidistant from the beams of the sides of the angle, in our case these are the sides of a triangle enclosing the angle. If we want to draw a circle in a triangle, we need to find a point that is equidistant from all three sides. This is done by drawing a bisector to each of the angles of the triangle.
The point where the bisectors of the angles intersect represents the centre of the triangle of the drawn circle. The sides of a triangle are exactly half a radius away from this point, so a circle drawn with each of them will have exactly one common point.
The circle can be drawn on a quadrilateral (chord quadrilateral):
The quadrilateral has opposite angle supplementary:
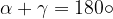
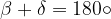
The circle can be drawn in a quadrilateral (tangent quadrilateral):
In a tangent quadrilateral, the sum of the lengths of the two opposite sides is equal to the sum of the lengths of the other two opposite sides:
Any n-angle polygon can be inscribed or circumscribed in/on a circle.
The figure below shows an example for a right hexagon. The polygon is inscribed on the blue circle but circumscribed on the red circle:
