A circle is a set of points T in a plane that are equidistant from the centre C. Mathematically, this can be written as:
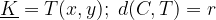
We draw a circle with centre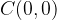 
and radius 
:
The point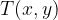 
lies on a given circle exactly when its distance from the origin is equal to r. We see that the radius we are looking for is the hypotenuse of a right triangle 
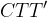with the sides x and y, so Pythagoras' theorem holds:
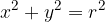
The point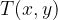 
lies on a given circle exactly when its coordinates z and y satisfy the above equations. If the point 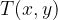does not lie in the first quadrant, the length of the sides of the right angle triangle is equal to 
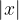and 
, and 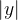an equivalent equation is obtained for squaring.
The equation of a circle with centre at the coordinate origin S (0, 0) and radius r is:
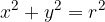
The centre of the circle can also be outside the coordinate origin, e.g. at point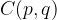 
. We draw a circle with centre 
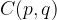and radius r:
The point 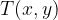lies on this circle exactly when 
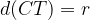or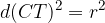 
, respectively:
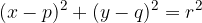
The equation of a circle with centre 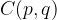and radius 
is therefore:
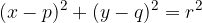
The equation of a circle with centre 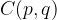and radius r can also be written in general form:
The equation of a circle with centre 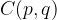and radius r in general form is therefore:
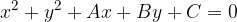
The point and the circle can be in different positions:
A circle with centre and radius 
We see that the point 
lies on the circle. The distance of the point from the centre of the circle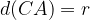 
. Which can also be written differently:
The point lies on a circle with radius r centre 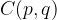if:
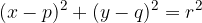
The point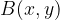 
lies inside the circle. The distance of the point 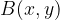from the centre of the circle 
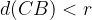. Therefore:
The point 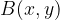lies inside a circle of radius r the centre of 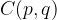if:
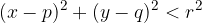
The point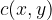 
lies on the outside of the circle. The distance of the point 
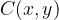from the centre of the circle 
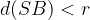. Therefore:
The point 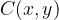lies on the outside of a circle of radius r the centre o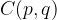f if:
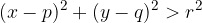
We are interested in the intersection of the circle 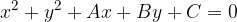and the line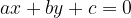 
We express one variable from the line equation:
We insert this variable into the equation of the circle:
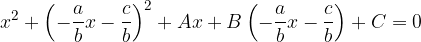
We get the quadratic equation:
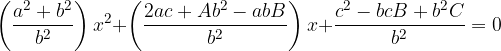
The following situations are possible:
in the first case
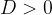
The quadratic equation has two real solutions, so the line and the circle have two points in common.
in the second case
the quadratic equation has one real solution, so the line and the circle have one common point; the line is tangent to the circle.
in the third case
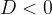
this quadratic equation has no real solutions so the line and the circle have no points in common.
