A spherical planet has mass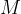 
and radius 
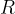. The planet may be assumed to be isolated in space and to have its mass concentrated at its centre. The planet spins on its axis with angular speed 
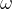, as illustrated in the figure below.
A small object of mass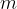 
rests on the equator of the planet. The surface of the planet exerts a normal reaction force on the mass.
State a formula in terms of 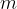, , 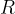and 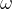, for the centripetal force required for circular motion of the small mass.
The radius of the planet is 
. It completes one revolution in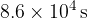 
. Calculate the magnitude of the centripetal acceleration at
the equator,
one of the poles.
.
.
