

Combinations are arrangements of n elements in r places. Basically these are arrangements where we ignore the order.
In combinations, order does not matter.
Combinations without repetition are used when we want to arrange r elements from a set of n elements in different ways. In doing so, we must make sure that these elements are different and do not repeat themselves.
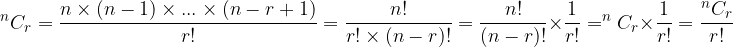
Here we have now proved that combinations are essentially Permutations, where we neglect the order.
We have a set with n different elements and from it we select r different elements with which we want to form different combinations, where the order is not important.
The number of combinations without repetition is calculated as follows:
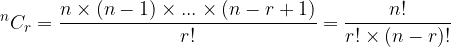
The term  can also be written with a binomial symbol, ie:
can also be written with a binomial symbol, ie:
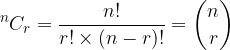
Repetition combinations are used when we want to arrange r elements from a set with n elements in different ways. In doing so, the same element can occur as many times as desired.

We have a set with n elements and from it we select r elements with which we want to form different combinations, where the order is not important and the same element can appear several times.
The number of repetitive combinations is calculated as follows:
