Personal collections


When we want to find the square root of a negative number, for example 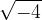 , or to find which number multiplied by itself gives a negative result, for example
, or to find which number multiplied by itself gives a negative result, for example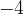 , we run into a problem (obviously neither 2 nor - 2 is the right answer). The answer can be obtained by introducing complex numbers.
, we run into a problem (obviously neither 2 nor - 2 is the right answer). The answer can be obtained by introducing complex numbers.
A complex number is a new number that we have not yet known. Let’s take a look at how it’s put together below.
Let us expand the largest set of real numbers to date. To this end, we first introduce a new, imaginary unit 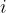 .
.
The imaginary unit i is defined as:
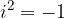
An erroneous definition of an imaginary unit often occurs in the form:
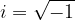
since the square root is defined only for nonnegative numbers. That the above form is incorrect is evident from the following contradictory example:
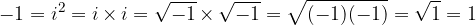
The imaginary unit i allows the evaluation of negative numbers below the square root. Let's look at this in a concrete example.
Each square root of a negative number can therefore be written in an imaginary unit form:
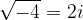
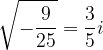
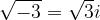
and so on.
All obtained numbers have the form:

We call them imaginary numbers.
The complex number consists of two parts:
The real and
the imaginal parts.
In general, we write it as the sum:
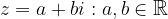
where:
When determining the imaginary component of a complex number, we take care to determine it correctly:
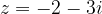 is an imaginary component of
is an imaginary component of 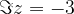 and not
and not 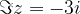
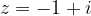 is an imaginary component of
is an imaginary component of  and not
and not 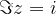 .
.
The set of complex numbers  therefore represents an extension of the real numbers
therefore represents an extension of the real numbers  , in which we can also root negative numbers:
, in which we can also root negative numbers:
For the real component of the complex number  we will use the following symbols:
we will use the following symbols:

We will use the following notation for the imaginary component of the complex number  :
:

All symbols are identical.
We illustrated the real numbers on the number axis. These numbers occupy the entire axis. When we want to introduce imaginary numbers, which also have new properties in relation to real numbers, we must refer them to a new, imaginary axis.
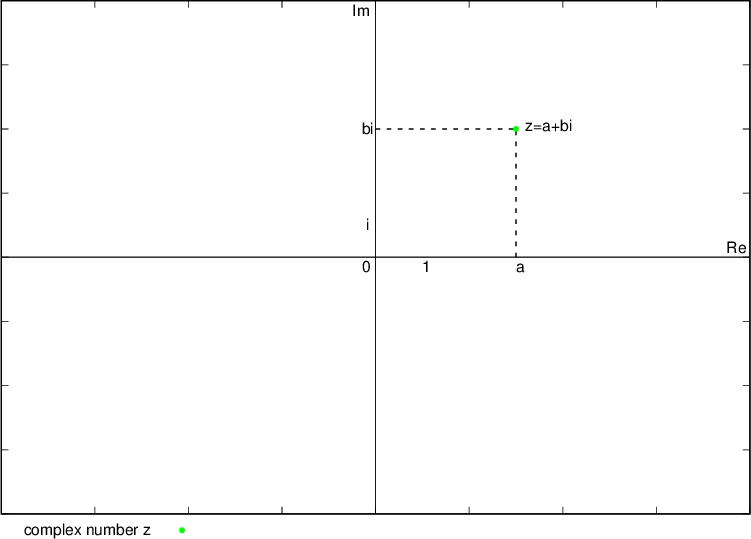
Complex numbers are geometrically illustrated in the complex plane.
The basis of a complex plane is a rectangular coordinate system:
We illustrate real numbers on the abscissa axis. We call it the real axis and denote it by Re.
We illustrate imaginary numbers on the ordinate axis. We call it the imaginary axis and denote it by Im.
The complex number z, which is a pair of real and imaginary numbers, is illustrated in a complex plane with a point. Its abscissa is equal in value to the real component, and its ordinate to the imaginary component of the complex number. The reverse is also true: each point of a complex plane corresponds to exactly one complex number.
Let us look at some sets of points 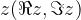 in a complex plane for which the coordinates
in a complex plane for which the coordinates  and
and 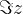 correspond to certain conditions:
correspond to certain conditions:
If in the condition the sign is  or
or 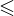 , the solution is the area of the complex plane including its edge (drawn with a solid line).
, the solution is the area of the complex plane including its edge (drawn with a solid line).
If the condition is the sign  or
or  , the solution is an area of a complex plane without its edge (drawn with a dashed/broken line).
, the solution is an area of a complex plane without its edge (drawn with a dashed/broken line).
Numbers whose real part is  lie on a line parallel to the imaginary axis and passes through the complex number
lie on a line parallel to the imaginary axis and passes through the complex number 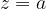 , i.e. the point
, i.e. the point 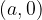 :
:
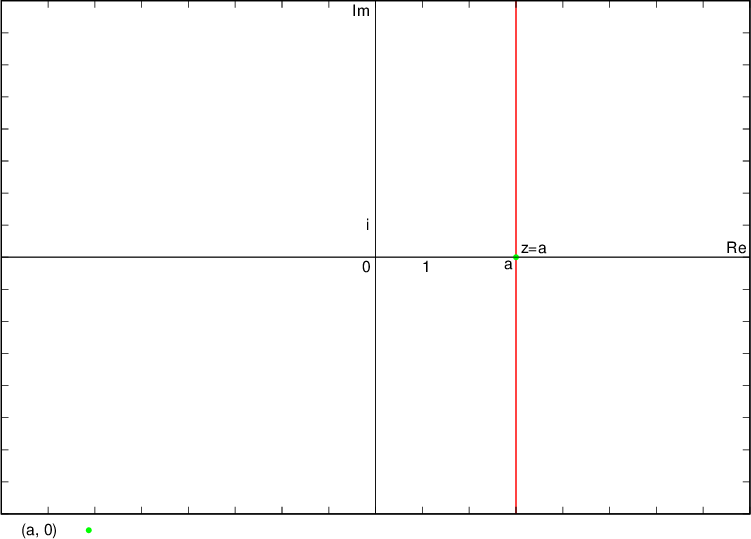
The numbers whose real part is 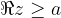 lie on the line and to the right of the line (hence the line drawn with a solid line), which is parallel to the imaginary axis and goes through the complex number
lie on the line and to the right of the line (hence the line drawn with a solid line), which is parallel to the imaginary axis and goes through the complex number 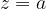 , i.e. the point
, i.e. the point 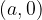 :
:

Numbers whose real part is 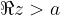 lie to the right of the line (hence the line drawn with a dashed line) parallel to the imaginary axis and passing through the complex number
lie to the right of the line (hence the line drawn with a dashed line) parallel to the imaginary axis and passing through the complex number 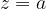 , i.e. the point
, i.e. the point 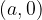 :
:
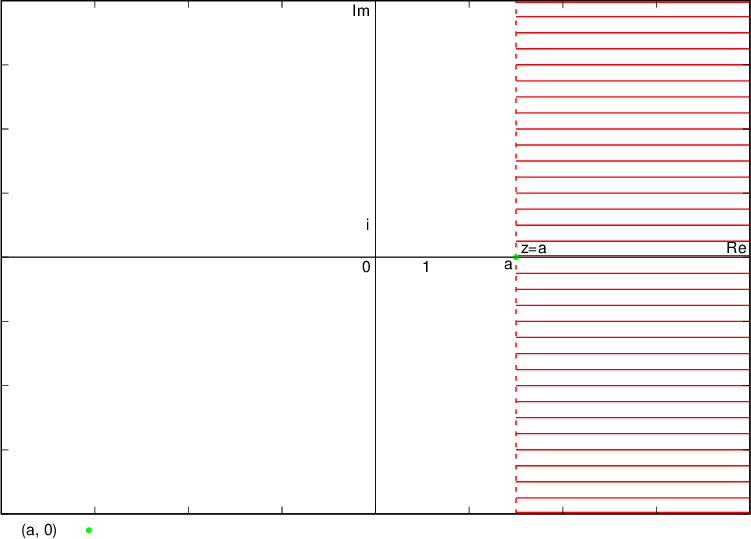
The numbers whose real part is 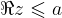 lie on the line and to the left of the line (hence the line drawn with a solid line), which is parallel to the imaginary axis and goes through the complex number
lie on the line and to the left of the line (hence the line drawn with a solid line), which is parallel to the imaginary axis and goes through the complex number 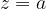 , i.e. the point
, i.e. the point 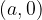 :
:

Numbers whose real part is 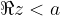 lie to the left of the line (hence the line drawn with a dashed line) parallel to the imaginary axis and passing through the complex number
lie to the left of the line (hence the line drawn with a dashed line) parallel to the imaginary axis and passing through the complex number 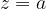 , i.e. the point
, i.e. the point 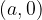 :
:

Numbers whose imaginary part is 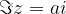 lie on a line parallel to the real axis and passes through the complex number
lie on a line parallel to the real axis and passes through the complex number 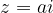 , i.e. the point
, i.e. the point 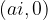 :
:
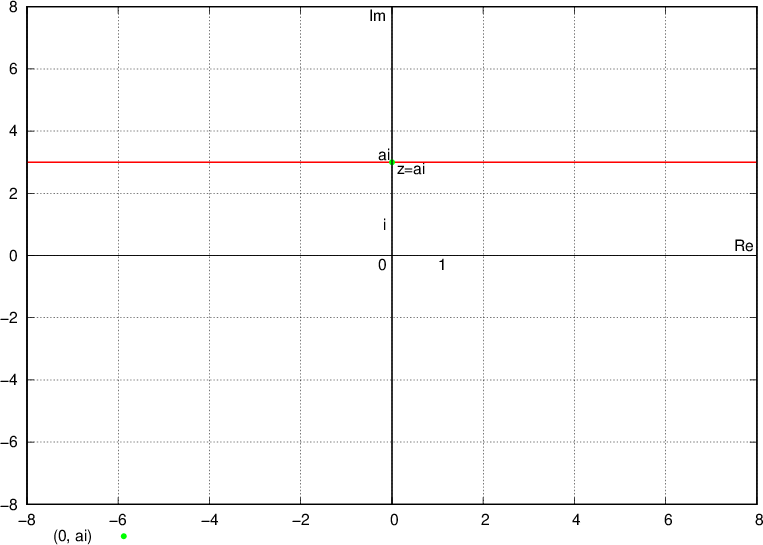
Numbers whose imaginary part is 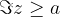 lie on a line and above a line (hence a line drawn with a solid line) parallel to the real axis and passing through the complex number
lie on a line and above a line (hence a line drawn with a solid line) parallel to the real axis and passing through the complex number 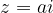 , i.e. point
, i.e. point 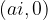 :
:
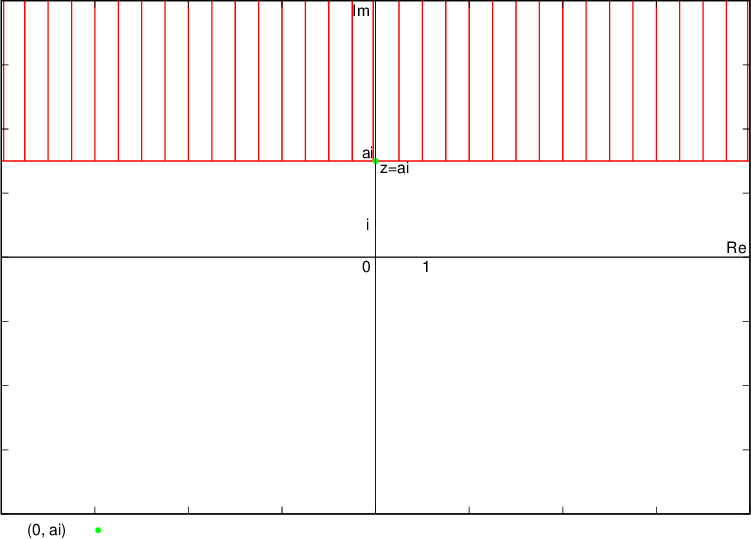
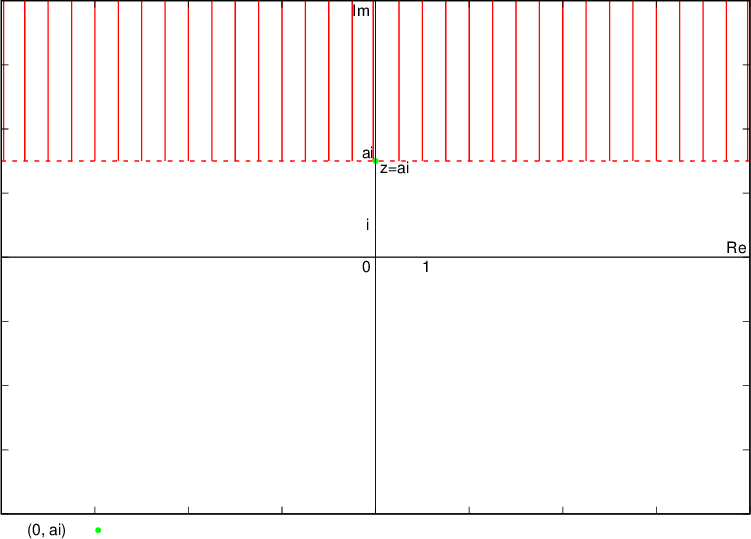
Numbers whose imaginary part is 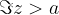 lie above the line (hence a line drawn with a solid line) that is parallel to the real axis and goes through the complex number
lie above the line (hence a line drawn with a solid line) that is parallel to the real axis and goes through the complex number 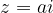 , i.e. point
, i.e. point 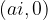 :
:
Numbers whose imaginary part is  lie on a line and below a line (hence a line drawn with a solid line) that is parallel to the real axis and goes through the complex number
lie on a line and below a line (hence a line drawn with a solid line) that is parallel to the real axis and goes through the complex number 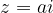 , i.e. the point
, i.e. the point 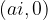 :
:
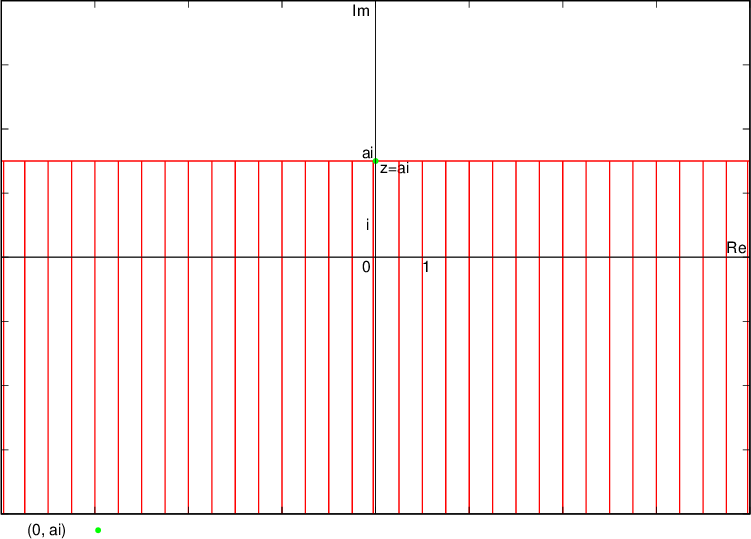
Numbers whose imaginary part is 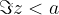 lie below the line (hence the line drawn with a dashed line) parallel to the real axis and passing through the complex number
lie below the line (hence the line drawn with a dashed line) parallel to the real axis and passing through the complex number 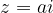 , i.e. the point
, i.e. the point 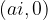 :
:
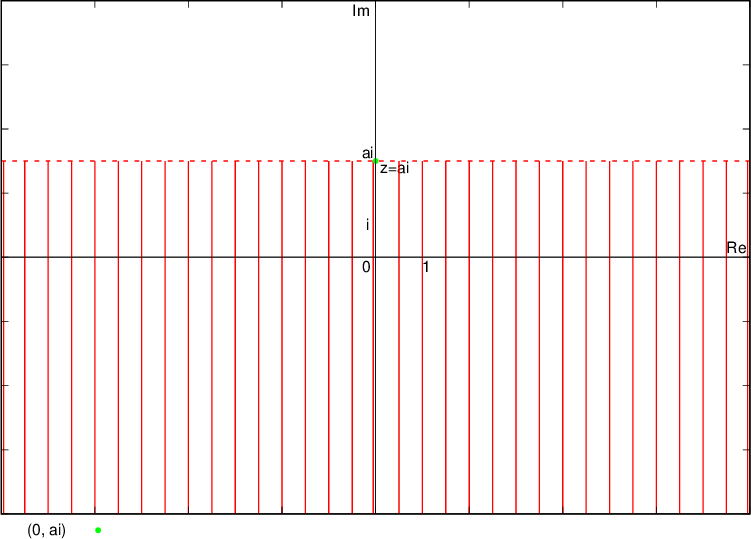
Numbers whose real part corresponds to the condition 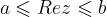 lie on lines (therefore lines are drawn with solid lines) and a plane band between lines, which are parallel imaginary axes and go through the complex numbers
lie on lines (therefore lines are drawn with solid lines) and a plane band between lines, which are parallel imaginary axes and go through the complex numbers 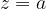 and
and  true points
true points 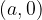 and
and 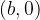 :
:

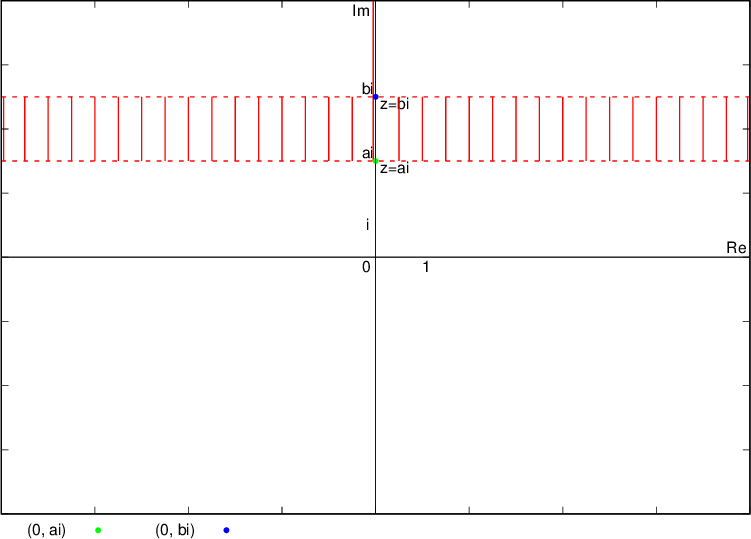
Numbers whose imaginary part corresponds to the condition 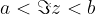 lie on the plane band between the lines (so the lines are drawn with dashed lines) that are parallel to the real axis and go through the complex numbers
lie on the plane band between the lines (so the lines are drawn with dashed lines) that are parallel to the real axis and go through the complex numbers 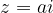 and
and 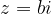 , say
, say 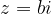 , se
, se
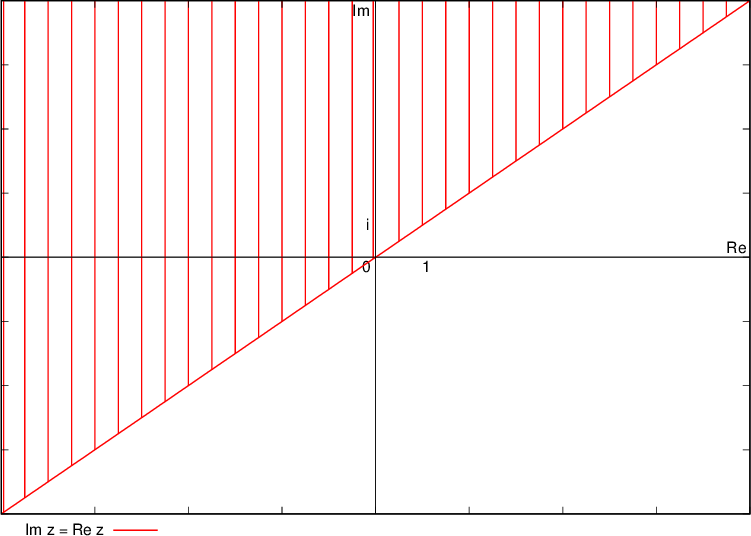
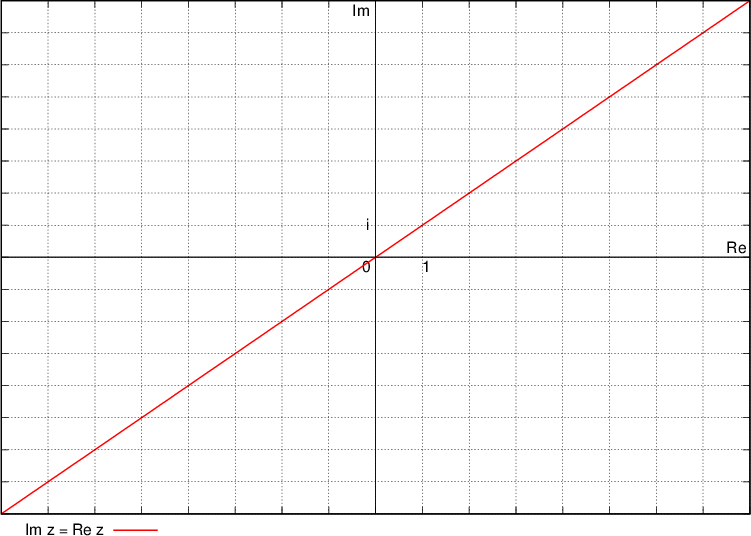
The numbers corresponding to the condition 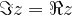 , that is, their imaginary component is equal to the real component, lie on the symmetry of the odd quadrants:
, that is, their imaginary component is equal to the real component, lie on the symmetry of the odd quadrants:
Namely, if we denote the real component as x and the imaginary as y, we can write the above condition as y = x. This, in turn, is the equation of the bisector of the odd quadrants.
The numbers corresponding to the condition 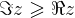 , ie their imaginary component is larger than the real component, lie on the bisector (so the bisector is drawn with a solid line) and above the bisector of the odd quadrants:
, ie their imaginary component is larger than the real component, lie on the bisector (so the bisector is drawn with a solid line) and above the bisector of the odd quadrants: