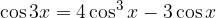The sum and difference of angle identities are often used to rewrite expressions in other forms or to rewrite an angle in terms of simpler angles. Additionally, these identities can be used to simplify expressions or prove new identities.
Sine:
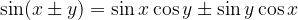
Cosine:
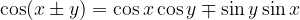
Tangent:
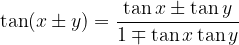
Sine:
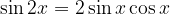
Cosine:

Tangent of double angle
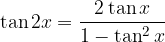
Sine of the half angle:
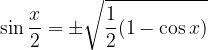
Cosine of half-angle:
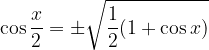
Tangent of half-angle:
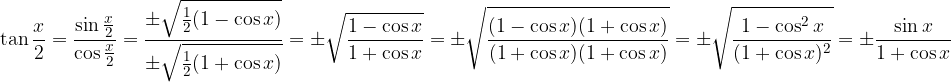
Using the addition theorems, we derive the formulas for 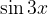 and
and 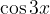 .
.
Let's derive the identity:
Therefore,

Let's derive an identity for cos 3x:
Therefore,