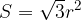A cone is a geometric body whose surface consists of a round flat surface over which a curved surface is wrapped. The tip always stands opposite the round flat surface. A flat surface is called the base surface, and the tip is called the top of the cone.
The cones are divided into two groups:
upright - the top lies just above the centre of the base area and
oblique - the top is offset from the centre of the base area.
As we have seen, we know the upright and the oblique cone, and we may ascribe some common features to both.
A cone is a round geometric body bounded by a base and lateral surface:
The cone is characterized by the following elements:
Base of a cone is a flat face which is a circle.
The axis of a cone is a line passing through the centre of the base, through the top of the cone.
The height of the cone is the distance between the base and the top of the cone. Height is the line perpendicular to the base.
A cone has a base, no edges and one vertex located at the top (apex).
The side of a cone is a line with one end at the base edge and the other end at the top of the cone.
In the introduction, we saw that we distinguished between upright and oblique cones. The oblique cones go beyond basic school frame, so we will focus only on the vertical cones.
In the following, we consider only the vertical cones.
A cone is upright if its axis is perpendicular to the base. The cone's base is a circle. The sides of the cone are the same length, so that the axial section represents an isosceles triangle.
The following features applies to an upright cone:
The lateral surface of the cone is the area covered by the curved surface.
The height of the upright cone lies on the axis of the cone.
The sides of the vertical cone are the same length.
These simplifications make it easier for us to calculate the area and volume of the cone, which we will learn about below.
The area of a cone is the sum of the areas of both surfaces bounding the geometric body. The boundary surfaces of a cone are geometric figures whose surfaces we already know how to calculate. Each character is located entirely on a single plane, and the surface of the cone is arranged in several planes. Therefore, the boundary surfaces of the cone are spread out on the plane for easier representation and calculation.
If the surface of the cone is unwrapped on a plane surface, we obtain a grid of the cone. The whole grid represents a composite geometric figure.
The surface of a shape spread out on a plane surface is called the grid of a geometric body.
Calculating the area of a cone can be thought of as calculating the area of a composite geometric figure. In doing so, we first calculate the areas of individual parts of the shape, and then add these areas.
The base of a cone is a circle, so we can write:
The area of the base of the cone  is equal to the area of the circle representing the base:
is equal to the area of the circle representing the base:

where  is the radius of the base of the cone.
is the radius of the base of the cone.
The lateral surface of an upright cone has the shape of a sector of a circle. The length of the sector is equal to the circumference of the base, and the radius is equal to the side of the cone:
Let's derive the equation for the area of the lateral surface of an upright cone.
The equation for the area of the sector marked in the picture above is:

We want to write the equation without the angle 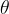 , so we express it with the radius of the side of the cone
, so we express it with the radius of the side of the cone 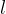 .
.
Let's start using the following ratio:
The ratio between the angle of the sector 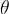 and the full angle is equal to the ratio of the sector S, versus the circumference of the entire circle C:
and the full angle is equal to the ratio of the sector S, versus the circumference of the entire circle C:
Let's write out the equation for the area of the sector:
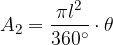
We continue with the derivation of the lateral surface of the vertical cone:
We have obtained the equation for the area of the lateral surface of the vertical cone.
The formula for the area of the lateral surface of the vertical cone is:
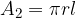
where  is the radius of the base, and
is the radius of the base, and 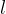 is the side of the cone.
is the side of the cone.
Now, let's derive the formula for the area of an upright cone. The area of the cone is the sum of the areas of the base and the lateral surface:

We have obtained the formula for the area of an upright cone.
The formula for the area of an upright cone is:
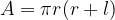
where  is the radius of the base, and
is the radius of the base, and 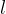 is the side of the cone.
is the side of the cone.
The volume of an upright cone is the size of space that the cone takes up.
The general equation for calculating the volume of an upright cone is:
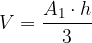
where 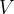 is the volume of the cone,
is the volume of the cone,  is the area of the base, and
is the area of the base, and 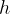 is the height of the cone.
is the height of the cone.
If we insert the area of the base into the formula, we get:
The formula for calculating the volume of an upright cone is:
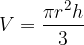
where  is the radius of the base, and
is the radius of the base, and 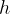 is the height of the cone.
is the height of the cone.
If we cut a cone at right angles to the base, and the plane passes through the vertex, you get an isosceles triangle called the axial section of the cone:
The base of an isosceles triangle represents the diameter of the base, and the legs represent the sides of the cone.
The axial section of a vertical cone is an isosceles triangle.
The base of an isosceles triangle represents the diameter of the base, and the legs the side of the cone.
The formula for calculating the area of the axial section of a vertical cone 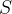 is:
is:

where  is the radius of the base, and
is the radius of the base, and 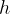 is the height of the cone.
is the height of the cone.
The axial section of an upright cone is an isosceles triangle. If we cut it into two halves perpendicular to the base, we get two right-angled triangles:
We can write out Pythagoras' theorem for both right-angled triangles:
When calculating the axial section of an upright cone, we use the Pythagorean theorem on a right triangle:
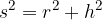
where  is the side,
is the side,  is the radius of the base, and
is the radius of the base, and 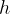 is the height of the cone.
is the height of the cone.
Cones are classified according to different properties, here are some special cases.
As we learned in the introduction, cones can be upright or oblique. The calculations for the oblique cones go beyond primary school framework.
This material deals in more detail only with upright cones.
An equilateral cone has sides equal to base surface diameter:
Area of an equilateral cone
Let's derive the equation for the area of an equilateral cone.
We start from the general equation for the area of a cone:
We have obtained the formula for the area of an equilateral cone.
The equation for calculating the area of an equilateral cone is:
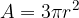
where  is the radius of the base of the cone.
is the radius of the base of the cone.
Volume of an equilateral cone
Let's derive the formula for the volume of an equilateral cone with the general equation for the volume of the cone:
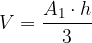
Before proceeding with the derivation, we express the height of the cone with the radius of the base.
Let's use the Pythagorean theorem from the axial section of a vertical cone:
Let's continue with the derivation of the lateral surface of a vertical cone:
We obtained the equation for the volume of an equilateral cone:
The equation for calculating the volume of an equilateral cone 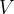 is:
is:
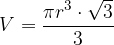
where  is the radius of the base of the cone.
is the radius of the base of the cone.
Axial section of an equilateral cone
The axial section of an equilateral cone is an equilateral triangle:
The side of an equilateral triangle is equal to the diameter of the base or the side of the cone.
Let's derive the formula for the area of the axial section of an equilateral cone.
We start from the general formula for the area of the axial section of a cone:

Let's insert the height 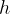 we earlier derived into the formula:
we earlier derived into the formula:
We have obtained the formula for the area of the axial section of an equilateral cone.
The area of the axial section of an equilateral cone 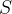 is:
is: