A polynomial is given as:
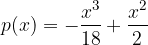
Calculate the initial point and turning point, then draw a graph of the polynomial.
The bisector of the odd quadrants bounded the polynomial curve into two regions. Prove that their areas of the regions are the same.
Let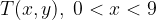 
, be the point on the graph of the polynomial 
and 
be the perpendicular projection of the point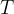 
on the abscissa. Calculate the abscissa of the point 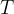at which the area of the triangle 
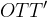is greatest. 
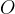is the origin of the coordinate system.
,
.
.
coordinate in which the triangle will have the largest area is:
