Personal collections


Intermolecular or interatomic forces act in matter. These are attractive forces. In fact, these are chemical bonds between molecules and atoms. The magnitude of such a force determines the aggregate state of a substance:
strong interatomic and intermolecular forces make a substance exist as a solid.
"medium strength" forces exist in liquids.
and weak forces which exist in gases.
Intermolecular forces are the basis of the electric force (see Forces in an Electric field - Coulomb's Law). How big they are depends on the substance itself, in what aggregate state the substance is (solid, liquid, gas), how it is crystallized, and also on the temperature of the substance.
How much force there is in a substance can be investigated by exerting an external force on the substance. An external force deforms the substance. The distances between the molecules increase or decrease - depending on the direction of the external force.
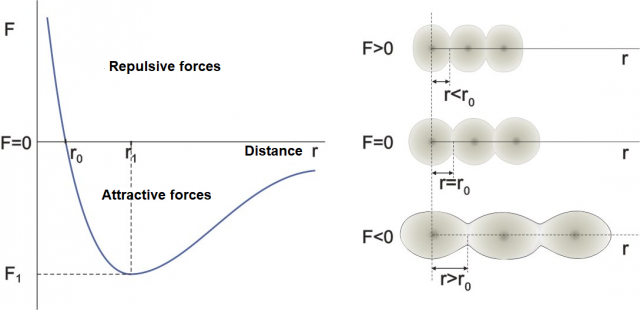
Figure 1: Dependence of the distance between atoms (molecules) on the direction and magnitude of the external force.
The graph on the left in Figure 1 shows how the distance between atoms or molecules changes depending on the external force. The graph on the right represents a model of atoms on which an external force acts. (The same would apply to molecules). The darker part in the figure is the nucleus of the atom, while the lighter part is the electron shell around the nucleus. If the substance is solid (or even liquid), the atoms are always in contact while only in gases they can be spaced apart.
Under the influence of an external force, they compress or stretch, so the distance  between them changes:
between them changes:
Point F = 0
If there is no external force, the distance between the atoms (molecules) is approximately equal to 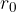 . Let's imagine the atoms in this case as spheres with radius
. Let's imagine the atoms in this case as spheres with radius 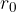 - Figure 1 middle right.
- Figure 1 middle right.
Region around F = 0
In a narrow area around 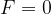 , the force is linearly dependent on the distance between molecules, which is written as:
, the force is linearly dependent on the distance between molecules, which is written as:
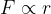
Region F > 0
A positive external force compresses the molecules - Figure 1, top right. In solids, the compression is strongly hindered by the electron shell around the nucleus of the atom. Electrons are negatively charged particles between which strong repulsive electric forces act (see Forces in an Electric field - Coulomb's Law). In order to bring two atoms closer together, we must cancel out the repulsive effect of electrical forces with a strong positive external force.
Region F < 0
A negative external force stretches the molecules -Figure 1, bottom right. The tension is opposed by the attractive forces between molecules and atoms - chemical bonds. The consequence of the stretching by the external force is that the molecules move apart - the distance  between them increases. At small forces, the distances increase linearly with the force but this becomes non-linear as the forces become bigger.
between them increases. At small forces, the distances increase linearly with the force but this becomes non-linear as the forces become bigger.
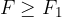
When the external force reaches a value  and the distance between the molecules is equal to
and the distance between the molecules is equal to  , the intermolecular force begins to weaken. The material begins to tear and the intermolecular force quickly drops to zero.
, the intermolecular force begins to weaken. The material begins to tear and the intermolecular force quickly drops to zero.
A force can act on a body at a single point, i.e. at the point of application of the force. Normally, a force does not act at a point, but is distributed over a certain area. The smaller the area on which the force acts, the greater the influence of the force on the deformation of the body. We say that the greater the pressure of the force.
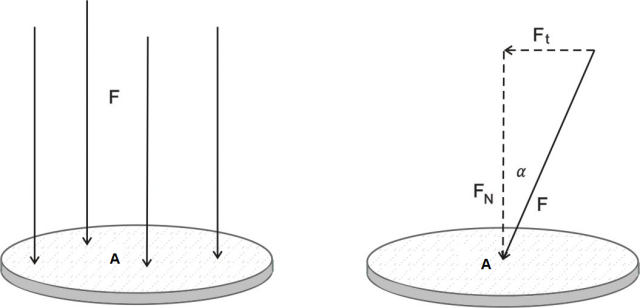
Figure 2:Force pressure. Left image: The force and the surface area are perpendicular. Right image: The force acts at an angle on the surface
The force pressure 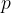 is the force
is the force  divided by the area
divided by the area 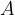 on which the force acts (Figure 2, left):
on which the force acts (Figure 2, left):

If the force is not perpendicular to the surface (figure 2, right), the force is resolved into two components:
the perpendicular or normal component  , and
, and
the transverse or tangential component 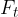 .
.
Pressure is only caused by a force perpendicular to the surface, tangential force causes shear stresses, which we will not discuss in this chapter.
Let's obtain the formula for the force pressure (only the perpendicular component is taken into consideration!):
The unit of pressure is the pascal [Pa]:
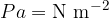
The larger unit is the bar:
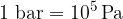
The pressure is:
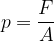
If the force is not perpendicular to the surface, we take the perpendicular component of the force:
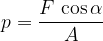
The unit of pressure is  or Pa (Pascal). The larger unit is the bar:
or Pa (Pascal). The larger unit is the bar:
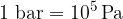
Let's now reverse the direction of the force so that it stretches the object (see Figure 3). A tensile stress is acting on the body and this is equal to the quotient of the force  and the area
and the area 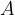 .
.
The tensile stress is denoted by  .
.

The unit of tensile stress is the same as for pressure: the pascal (Pa).
We calculate tensile stress in the same way as pressure, only we use the symbol  instead of
instead of 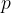 :
:

The unit is also the same as for the pressure, i.e. pascal [Pa].
Under the influence of tensile stress, a body extends or stretches - see Figure 4.
Let us first observe how the tensile stress  affects the extension
affects the extension 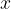 of the rod. Let the original length of the rod be
of the rod. Let the original length of the rod be 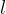 and we can define the relative extension of the rod as:
and we can define the relative extension of the rod as:
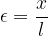
This is called the tensile strain and is denoted by  . It has no unit, as the units in the numerator and denominator cancel out each other.
. It has no unit, as the units in the numerator and denominator cancel out each other.
For relatively small tensile stresses, a linear relationship between tensile stress  and tensile strain
and tensile strain  occurs:
occurs:

The notation  is called Young's modulus of elasticity. It depends only on the chosen substance and not on the shape of the body. It tells us how much tensile stress is required for a given strain:
is called Young's modulus of elasticity. It depends only on the chosen substance and not on the shape of the body. It tells us how much tensile stress is required for a given strain:
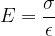
The unit for the modulus of elasticity is  .
.
Figure 5 shows the dependence of tensile stress on the strain.
The graph in Figure 5 is divided into four sections:
Linear section
Equation 1 applies in the linear section. The rod stretches linearly up to a point called the limit of proportionality. If we reduce the tensile stress to 0 at any point in this range, the bar will return to its initial, unstretched, state.
Non-linear section
When the rod is stretched beyond the limit of proportionality - but not beyond the elastic limit, equation 1 is no longer valid. Equation 1 is only a linear approximation, but in the given range nonlinear terms also appear.
Equation 1 is no longer valid, but if the tensile stress is reduced to 0, the rod will still return to its initial, unstretched, state.
Plastic deformation
If the elastic limit is exceeded but the yield point is not exceeded, the rod is plastically (permanently) deformed. This means that even if we reduce the tensile stress to 0, the rod does not return to its initial unstretched state, but remains permanently stretched (see the dashed line in Figure 5).
Breaking point
If we exceed the yield point, the rod breaks. This means that the rod continues to stretch at a constant tensile stress. With further stretching, the cross-section of the rod becomes smaller and, therefore, at the same force, a lower tensile stress is required for greater deformation of the rod. The rod is stretched even though the tensile stress drops.
We have reached the yield point. If the tensile stress is not removed at this point, the rod will surely collapse (break, shatter, split...). For an explanation of the phenomenon of the collapsing rod, see also the introductory chapter - Figure 1.
A material stretches under the influence of tensile stress. In the linear extension region, the equation below holds:
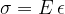
 is the modulus of elasticity, which depends only on the substance. Here, the tensile strain
is the modulus of elasticity, which depends only on the substance. Here, the tensile strain  is given as:
is given as:
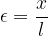
The pressure 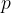 acts on a rod so that it contracts - Figure 6.
acts on a rod so that it contracts - Figure 6.
The pressure causes the length of the rod to decrease by 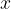 . Even now, equation 1, which we wrote down in the previous chapter, applies, at least as long as we are in the linear section, except that instead of tensile stress
. Even now, equation 1, which we wrote down in the previous chapter, applies, at least as long as we are in the linear section, except that instead of tensile stress  , we use the pressure
, we use the pressure 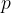 :
:
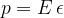
where  :
:
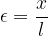
But what if there is force pressure from all directions on the body? In this case, the body is compressed, and its volume 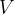 decreases by
decreases by 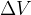 , as shown in Figure 7.
, as shown in Figure 7.
The relative decrease in volume is proportional to the change in pressure on the body:

The sign (-) means that the volume decreases at higher pressure.
The proportionality constant 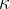 (pronounced kappa) represents the compressibility of the substance. The unit is
(pronounced kappa) represents the compressibility of the substance. The unit is 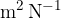 . In the case of solid substances and also liquids, the compressibility is very low.
. In the case of solid substances and also liquids, the compressibility is very low.
The relative change in volume of a body is proportional to the pressure acting on the entire body.
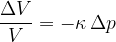
The proportionality constant 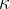 is called the compressibility of the substance the body is made of and it depends only on the selected substance, not on the geometry of the body.
is called the compressibility of the substance the body is made of and it depends only on the selected substance, not on the geometry of the body.