The use of the derivative was discussed in a previous chapter on polynomials and rational functions. In the following, we will look at the derivatives of some other functions.
We know from theory that the composite of the function can be written as:
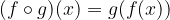
the obtained result is called composite function, which works by first mapping the initial element with the function g, and then obtaining the obtained element with the function f.
Now let's look at the derivative of the composite function. Take the case where we have a function that we do not know how to derive directly. In this case, the composite comes in handy, because a given function can be written as a composite function of two functions that we know how to derive. Let's look at the rule for the derivative of a composite or a composite function:
Let the function f be derivable at the point x, and the function g be derivable at the point f (x). Then, at the point x, the composite function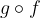 
is also derivable and applies:
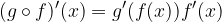
Given a root function:
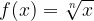
Let's separate it:
Derivative of the root function
is the same
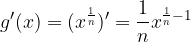
In a similar way we can find the derivative of the function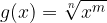 
:
We derive the function:
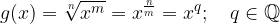
is the same
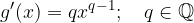
First, let’s repeat what an implicit function is. We know that the shape function is explicitly given
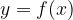
which can be written in implicit form:
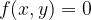
So far, we have learned to derive explicitly written functions. Sometimes, however, we have a given function in an implicit form that cannot be easily converted to an explicit form. So let’s consider how we could derive the function in an implicit form.
Basically, we approach the derivation of an implicit function as follows:
We derive both sides of the equation.
Since y depends on x, y is derived as an indirect function.
Express the derivative y '.
