

The difference of squares is a term often encountered in mathematics. We recognize it as two squared terms, between which there is a minus sign.
The difference of squares is especially important in mathematics.
In the following, we will learn how to factorise the difference of squares. We will need this method to simplify fractions. All fractions can be simplified only when there are only products in the numerator and denominator.
Factorising the difference of squares gives the product of the sum and difference of two equal terms.
We write the general formula (equality) for the difference of squares.
The difference of the squares is equal to the product of the sum and the difference of two identical terms:
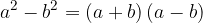
Let's factorise another difference of squares by the formula.
Sum of squares:
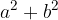
cannot be factorised.