Personal collections


Divisibility is the relation between numbers. Let 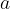 and
and 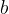 be numbers. We say that
be numbers. We say that 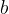 divides
divides 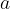 if there exists such a number
if there exists such a number 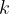 such that:
such that:
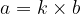
or, 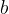 divides
divides 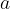 if
if 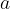 is a multiple of
is a multiple of 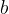 .
.
The above equality 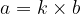 can also be transformed into a more familiar form:
can also be transformed into a more familiar form:
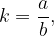
where
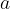 is called divisor
is called divisor
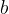 is called dividend
is called dividend
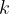 is called quotient.
is called quotient.
The divisibility relation between numbers is denoted by:
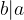
and read as: b divides a.
There are infinites of multiples of any number, and there are finally many divisors.
We say that a relation is reflexive because each number is considered to divide itself.
If 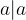 , then
, then  .
.
We say that a relation is antisymmetric because it holds that if two numbers divide each other, then the numbers are the same.
If 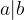 , and
, and 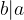 , then
, then 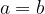 .
.
We say that a relation is transitive because it holds that when a number 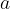 divides the number
divides the number 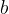 and that same number
and that same number 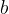 divides the number
divides the number  , then the number
, then the number 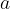 also divides the number
also divides the number  .
.
If 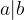 , and
, and 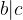 , then
, then 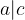 .
.
The definition of divisibility can be extended to integers. Let 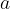 and
and 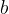 be integers. The number
be integers. The number 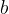 divides the number
divides the number 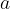 if there exists an integer
if there exists an integer 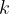 that is valid.
that is valid.
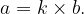
It is also true that 0 is divisible by any non-zero integer 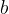 , since
, since
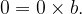
Each integer 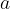 has at least 4 divisors:
has at least 4 divisors:
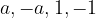
Let 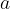 and
and 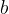 be natural numbers. Then, their:
be natural numbers. Then, their:
sum:
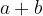
product:

are natural numbers, but the quotient is not necessarily a natural number. When the quotient is a natural number, we know that the numbers 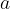 and
and 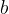 are in the divisibility relation, otherwise they are not in the relation and do not return a natural number to us when dividing.
are in the divisibility relation, otherwise they are not in the relation and do not return a natural number to us when dividing.
Regardless of the fact whether two natural numbers are in the divisibility relation or not, for all pairs of natural numbers 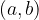 , where
, where 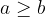 , we can write the basic theorem on division.
, we can write the basic theorem on division.
The basic theorem on division says that the division of any two natural numbers 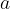 and
and 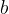 , to which
, to which 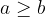 and
and 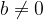 apply, can be written as
apply, can be written as
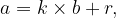
where:
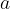 divisor
divisor
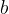 dividend
dividend
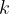 quotient
quotient
 remainder where
remainder where 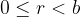 .
.