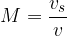Personal collections


A stationary sound source emits harmonic longitudinal waves. A receiver (observer), e.g., a microphone or an ear converts the wave into a harmonic oscillation of the diaphragm or eardrum. If the source of the wave and the observer are stationary, the observer detects (sound) at exactly the same frequency as the source emits. The observer detects a certain frequency based on the period - that is, the time between two compressions or rarefactions. The movement of the source or observer causes the time (period) between two compressions or rarefactions to change (see example) and thus the frequency we hear. This is called the Doppler effect.
We will explain the Doppler effect for four cases:
The sound source is stationary, the observer is approaching the source.
The sound source is stationary, the observer moves away from the source.
The sound source is moving and approaching a stationary observer.
The sound source is moving away from a stationary observer.
Let us consider the case when the observer approaches the source. It can be seen from the sketch that the distance between two successive compressions (or rarefactions, or in general, the wavelength of the sound emitted by the source) is divided into the distance travelled by the observer and the distance travelled by the sound:
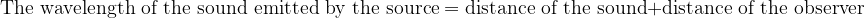
Let's write this mathematically:

where 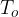 is the period of the sound detected by the observer. We know that the source is stationary and emits a sound of frequency
is the period of the sound detected by the observer. We know that the source is stationary and emits a sound of frequency 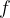 or period
or period  , and from the sketch, we can infer that:
, and from the sketch, we can infer that:
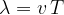
We have the needed equations, so let's calculate 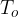 or
or 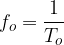 , which is the frequency of the sound received by the observer. From the two equations above, we have:
, which is the frequency of the sound received by the observer. From the two equations above, we have:
The derivation of the case when the observer moves away from the source is identical. The distance between the two wave backs appears to increase as the observer travels in the same direction as the wave. The frequency we hear is therefore lower:
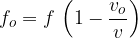
When the observer is moving and the source is stationary, the frequency  of the sound heard by the observer is given as:
of the sound heard by the observer is given as:
The source is stationary, the receiver is moving:
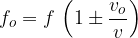
The + sign is used if the observer is approaching the source and - if it is moving away.
The source emits sound waves in the form of concentric circles. The movement of the sound source causes the centre of these circles to move as well. It seems that the wavefronts are compressed in the direction of movement of the source and stretched in the opposite direction of movement - see the figure below!
Let's take the example of a car moving towards a stationary observer.:
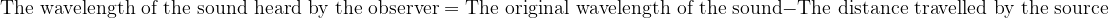
Write this in the form of an equation:
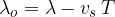
Where 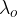 is the wavelength of the sound heard by the observer,
is the wavelength of the sound heard by the observer, 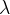 is the original wavelength of the sound emitted by the source,
is the original wavelength of the sound emitted by the source,  is the speed of the source and
is the speed of the source and  is the period of the original sound.
is the period of the original sound.
The frequency  and the wavelength
and the wavelength 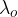 of the sound heard by the observer are related by the formula:
of the sound heard by the observer are related by the formula:
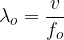
Using the set of equations above, let's now calculate the frequency of sound heard by the observer:
The same could be done for the case when the source is moving away from the stationary receiver and obtain the frequency  of the sound heard by the observer which will be:
of the sound heard by the observer which will be:
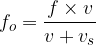
or
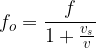
When the source is moving and the observer is stationary, the frequency  of the sound heard by the observer is given as:
of the sound heard by the observer is given as:
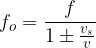
Minus sign (-) is used when the source is approaching the observer and + if it is moving away.
In the case of a moving source, we mentioned that the fronts are compressed in the direction of the source's movement and stretched in the opposite direction. Let's take a closer look at this phenomenon!
In the figure on the left, the velocity of the source is lower than the velocity of the wave. The centre of the concentric circles moves to the right with the speed  of the moving source and covers a distance
of the moving source and covers a distance 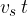 , the radius
, the radius 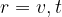 of the wavefronts increases in proportion to the wave speed
of the wavefronts increases in proportion to the wave speed 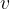 .
.
The figure in the middle shows a situation where the velocity  of the source is equal to the velocity
of the source is equal to the velocity 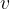 of the sound wave. The wave backs are compressed in the direction of movement of the source so that the distance between them becomes zero. We hear it as a bang. We say that the source of the sound (e.g. an airplane) has broken the sound barrier.
of the sound wave. The wave backs are compressed in the direction of movement of the source so that the distance between them becomes zero. We hear it as a bang. We say that the source of the sound (e.g. an airplane) has broken the sound barrier.
In the figure on the right, the source moves faster than the sound. The envelope of the wavefronts forms a Mach cone. The half angle of the top of the cone is equal to:
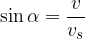
The fraction  is also called Mach (denoted by M).
is also called Mach (denoted by M).