In classical physics, the conservation law applies to mass, which states that mass cannot be destroyed or created from nothing. However, as Einstein discovered, this is not entirely true, as mass can be converted into energy and vice versa.
The proportion of mass that is converted into energy (or vice versa) during everyday phenomena in bodies is very small compared to the total mass of the body, so these changes are not detected even by the most accurate measuring devices. It is different for reactions in the nucleus, where these changes are large enough to be measurable.
The relationship between the mass of a body and the energy hidden in such mass was first determined by Einstein and is described by the equation:
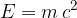
where:
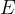is the energy that would be obtained if the entire mass 
were converted into energy,
is the mass of the body, and
is the speed of light, which is a constant and is given as:
.
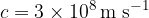If we add (or take away) some energy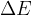 
from a body, maybe by, for example, heating, raising, or interacting with other particles, its mass increases (or decreases) at the same time as its energy and the change in mass 
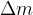is given as:
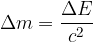
During reactions in the nucleus are:
the participating masses are small enough and
the energy that can be released is large enough
that the changes in mass can be measured.
As described in the material, Atomic nucleus, the mass defect of a nucleus is the difference between:
the total mass of free protons and neutrons in the nucleus, and
the mass of the nucleus with these same protons and neutrons combine.
This difference in mass is the result of the energy that is released during the formation of the nucleus or used to break it up.
The relationship between the change in mass 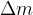and released or consumed energy 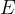is described by Einstein's energy equation as:
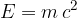
In the previous chapters, we described the mass of a body when energy is supplied to the body in the form of heat or potential energy. But what happens to the mass of the body if we supply it with kinetic energy and therefore accelerate it?
In the special theory of relativity, the total energy 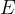of a body can be expressed as:
The energy of a moving body is therefore divided into:
the kinetic energy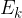 
, and
the energy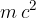 
of the body when it is at rest.
The last term, 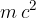, is called rest energy, and the mass of a stationary body is called rest mass. In the previous section, we saw that the rest mass of a body changes if we add or subtract (thermal or potential) energy from it using the equation:
In certain cases, we would also like to use the latter equation in the case of kinetic energy. We can do this by introducing relativistic mass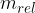 
and writing the energy as:
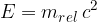
Let's take a closer look at what lies beneath the relativistic mass. In relativity theory, kinetic energy is no longer given as:
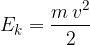
as is the case in classical physics, but instead becomes:
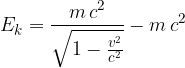
As stated earlier, the total energy is given as:
Such a generalized mass, however, depends on the speed. As the velocity increases, so does the relativistic mass of a body.
In the special theory of relativity, the total energy of a body can be written as:
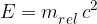
where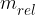 
is called the relativistic mass and is given as:
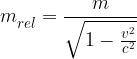
where is the rest mass of the body.
