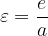An ellipse is the set of all points 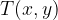 in the plane for which the sum of the distances from the two fixed points
in the plane for which the sum of the distances from the two fixed points  ,
,  is a constant.
is a constant.
The geometric definition of an ellipse can therefore be written as:
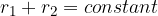
the geometric definition can be seen in the picture:
Mathematically, the equation of an ellipse as a second-order curve is characterized by the quadratic terms having the same sign and 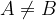 :
:
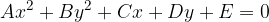
To make the explanation of characteristic elements of an ellipse easy, we have to use a sketch:
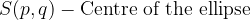
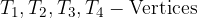

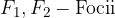

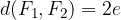
The ellipse has two poles:
Major pole: is the distance from the centre to the more distant apex; it is usually denoted by a. The foci of the ellipse always lie on the major pole.
Minor pole: is the distance from the centre to the less distant apex; it is usually denoted by b.
Another important property of an ellipse is numerical eccentricity, which is determined by:

The numerical eccentricity of the ellipse tells us how flattened the ellipse is. Numerical eccentricity always lies on the interval 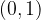 .
.
This chapter is not essential for understanding the material, so the reader may also omit it. It is intended for those students who want to deepen the material.
In deriving the equation, we will use the picture:
Let's start with the geometric definition of an ellipse:
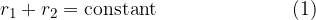
The first step we need to do is to determine the value of the constants. We can obtain the value of the constant by placing it in point B obtained from the diagram above:
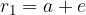
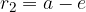
We then now insert 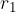 and
and 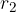 into the equation
into the equation 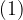 and get:
and get:
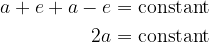
The obtained constant is inserted back into the original equation and we have:
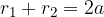
The next step is to express 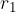 and
and 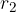 using the coordinates x and y. We do this with right triangles: the triangles
using the coordinates x and y. We do this with right triangles: the triangles 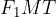 and
and  are right-angled, so we can write using the Pythagorean’s theorem:
are right-angled, so we can write using the Pythagorean’s theorem:
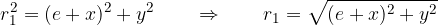
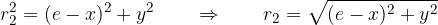
Let’s derive the equation of the ellipse:
The equation of ellipse in the central position is obtained as:
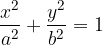
Equation of an ellipse with its centre at the coordinate origin in intercept form:
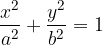
We can observe that if a = b, then the ellipse is converted to a circle.
The ellipse can be oriented in two different ways, namely:
Horizontal ellipse i.e., a> b.
Vertical ellipse i.e., b> a.
Let’s take a look at both orientations.
If the major pole of an ellipse is parallel to the x-axis, then the ellipse is said to be Horizontal ellipse.
The easiest way to explain the characteristic elements of an ellipse is to use a sketch:
From the sketch we see that the ellipse has vertices at points:
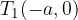


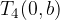
The foci of the ellipse are determined by the linear eccentricity e:
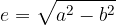
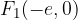
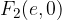
The numerical eccentricity of the ellipse is:
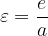
If the major pole of an ellipse is parallel to the y-axis, then the ellipse is said to be a Vertical ellipse. That is, b> a and the ellipse is stretched in the direction of the ordinate as shown below:
From the sketch we see that the ellipse has vertices at points:
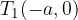


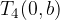
The foci of the ellipse are on the ordinate axis:
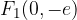

The linear eccentricity of the ellipse is calculated:

The numerical eccentricity of the ellipse is:
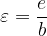
If we move the ellipse in parallel so that the centre reaches the point 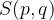 , the shifted ellipse has the equation:
, the shifted ellipse has the equation:
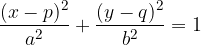
Let's take a look at the sketch of what a displaced ellipse looks like:
The ellipse in the displaced position has its centre at the point 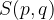
The characteristic points of the ellipse in the shifted position can be deduced from the sketch. We see that the ellipse has vertices at points:
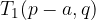

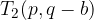

The foci of the ellipse are determined by the linear eccentricity e:
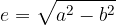
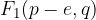
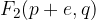
The numerical eccentricity of the ellipse is: