Personal collections


Exponential equations are equations with unknown exponent.
An exponential equation is usually encountered when we want to obtain the intersection of a graph of an exponential function with any other function like linear, quadratic and exponential functions e.t.c.
Exponential equations can be distinguished according to the methods by which they are being solved.
Some exponential equations can be simplified such that only powers with the same bases appear on both sides of the equation. That is:
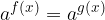
Such exponential equations can be solved by equating the exponents. That is:
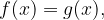
which follows from the injectivity of the exponential function.
These are the exponential equations in the form:

Graphs of exponential functions with different bases intersect on the ordinate axis, so the following must hold:

Some equations can be simplified by introducing a new unknown.
Equations in which exponential and non-exponential functions occur can only be solved graphically. For these equations, we first draw a graph of the two functions contained in the equation. We then obtain the solutions of the equation from the graph, and then confirm the solution with the calculations.
Exponential equations, where the sum or difference of powers of the same bases occurs, are solved by exposing the common factor. The equation is thus simplified into already known exponential equations.
Obtaining the logarithm of both sides solves equations of the type:

These are exponential equations that have different bases and different exponents on both sides. We’ll learn how to solve these equations in the previous sections.
Exponential inequalities are inequalities in which a unknown figure appears in the exponent. Inequalities are usually solved graphically. This means that we draw both graphs that appear in the inequality. But we can also be solved by calculation.