Personal collections


The first law of thermodynamics states that the change in the internal energy 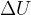 of an observed substance is equal to the added (or removed) heat
of an observed substance is equal to the added (or removed) heat 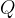 and work
and work 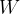 :
:

Heat energy is added e.g. by means of a gas burner or taken away by allowing it to cool.
The first law of thermodynamics states that the internal energy 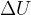 of a substance can change due to the heat quantity
of a substance can change due to the heat quantity 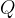 received (or emitted) and work
received (or emitted) and work 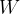 received or emitted:
received or emitted:
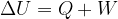
Work 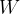 can be positive or negative:
can be positive or negative:
If the work is positive, we add internal energy to the substance. An example of positive work is if we rub iron against iron, for instance, using a saw or we compress the air into the inner tube of a wheel using a pump. In both cases, we do work, and therefore the internal energy of the substance increases. The body (or gas) heats up.
If a substance does work, that work is negative. According to the principle of energy balance for closed systems, this means that the internal energy of the substance decreases. An example is an iron rod that expands when heated and pushes another body away (does work).
The first law of thermodynamics applies to all substances. For simplicity, we will limit ourselves to an ideal gas.
We will observe separately what happens if the gas is heated at a constant volume (e.g. in a closed vessel) or at a constant pressure (which is determined, for example, by the force of the weight of the piston, which is pushed by the gas during expansion).
Let's take an ideal gas and heat it. First, it is heated in a closed vessel, i.e. at a constant volume - figure 1 a).
All the heating energy 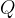 goes into the internal energy
goes into the internal energy 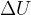 of the gas since the gas cannot expand to do work due to its constant volume, therefore:
of the gas since the gas cannot expand to do work due to its constant volume, therefore:
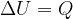
The heat 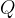 added at constant volume is given as:
added at constant volume is given as:
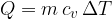
Therefore:

If a substance (ideal gas) is heated at constant volume, then no work has been done. The change in internal energy 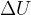 of the substance is therefore given as:
of the substance is therefore given as:
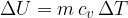
The index 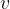 in the symbol
in the symbol  of the specific heat capacity simply indicates that the process is performed at a constant volume.
of the specific heat capacity simply indicates that the process is performed at a constant volume.
In the next step, we allow the gas to heat up and expand at constant pressure (Figure 1 b). In this case, according to the law of thermodynamics, the change in internal energy 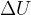 is equal to the sum of the supplied heat quantity
is equal to the sum of the supplied heat quantity 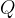 at constant pressure and the work
at constant pressure and the work 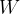 done by the substance during expansion.
done by the substance during expansion.
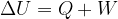
The heat 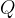 added at constant pressure is given as:
added at constant pressure is given as:

The index  in the symbol
in the symbol  of the specific heat capacity simply indicates that the process is performed at a constant pressure.
of the specific heat capacity simply indicates that the process is performed at a constant pressure.
When the gas expands, its volume increases and it does work, e.g. moves the piston some distance. For work 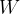 done, its internal energy is reduced, so the work is negative:
done, its internal energy is reduced, so the work is negative:

If we substitute equations 3 and 4 into equation 1, we have:
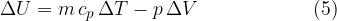
The internal energy of the heated gas at constant pressure increases by the heat supplied and decreases by the work done by the gas during expansion.
If a substance (ideal gas) is heated at constant pressure, it heats up and expands and therefore does work. The change in its internal energy is given as:
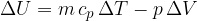
If we substitute equation 2 into 5, we can derive the relationship between the specific heat capacity 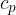 at constant pressure and the specific heat capacity
at constant pressure and the specific heat capacity 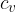 at constant volume.
at constant volume.
Let's imagine that we heat the system in the same way, first at a constant volume and then at a constant pressure. The change in internal energy is the same in both cases:
The specific heat capacity at constant pressure is always greater than at constant volume. At constant pressure, the gas expands and does the work.
For an ideal gas, the relationship between the specific heat capacities at constant pressure and constant volume is given as:
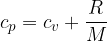
where 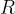 is the general gas constant and
is the general gas constant and 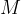 is the kilomolar mass.
is the kilomolar mass.
Let's write again equation 6 above:
The ratio of the specific heat capacity 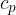 at constant pressure to the specific heat capacity
at constant pressure to the specific heat capacity 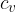 at constant volume is denoted by the Greek letter kappa
at constant volume is denoted by the Greek letter kappa 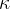 :
:

For a monatomic gas, this ratio is given as:
For an ideal monatomic gas, the relationship between the specific heat capacities at constant pressure and constant volume is given as:
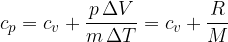
The specific heat capacity 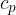 at constant pressure is given as:
at constant pressure is given as:
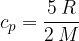
The specific heat capacity 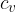 at constant volume is given as:
at constant volume is given as:

The ratio is given as:

Let's write equation 6 again:
Air can roughly be considered a diatomic gas, as nitrogen  and oxygen
and oxygen  molecules predominate. In the case of a diatomic gas:
molecules predominate. In the case of a diatomic gas:
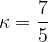
The specific heat capacity 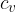 at constant volume is given for any ideal gas, as:
at constant volume is given for any ideal gas, as:
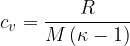
In the case of a diatomic gas:
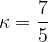
The result is approximately the same as the value given in the task.
For some gases,  ,
,  and
and 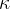 are given in the table below:
are given in the table below: