Personal collections


We want to push a load onto a truck. For this purpose, we lean the loading ramp against the truck. A loading ramp is a ramp that helps us get the box onto the truck with less force than if we were to lift it vertically.
We need to overcome two forces by pushing the load with our hands:
the dynamic component 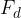 of the weight of the load; this is the force pushing the load down the plane, and
of the weight of the load; this is the force pushing the load down the plane, and
the frictional force 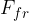 acting in the opposite direction to the motion of the load as we push, i.e. also down the plane.
acting in the opposite direction to the motion of the load as we push, i.e. also down the plane.
How do we calculate the frictional force acting against the motion of the load on the plane? What and how much is the dynamic force? With what force must we push the load up the plane so that it moves uniformly and in a straight line? All these are just some of the questions that we will answer in this material.
A body of mass 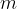 stands on an inclined plane.
stands on an inclined plane.
The force of the weight 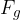 of the body acts vertically downwards. Let's resolve it into two components:
of the body acts vertically downwards. Let's resolve it into two components:
static component: the first component is perpendicular to the plane. We call it the static component 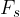
dynamic component: the second component is parallel to the plane. We call it the dynamic component 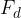 . It is also the component of the weight of the body that pushes it down the plane.
. It is also the component of the weight of the body that pushes it down the plane.
Let's see how we calculate them. We make a sketch:
In Figure 2, we can see we have two similar right-angled triangles:
the first triangle is coloured yellow and has legs with lengths  and
and 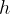 and a hypotenuse of length
and a hypotenuse of length  . It represents the inclined plane itself. In this triangle,
. It represents the inclined plane itself. In this triangle, 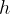 is the height and
is the height and  is the length of the plane. The angle between the leg with length
is the length of the plane. The angle between the leg with length  and the plane is
and the plane is 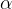 . The other angles are shown in Figure 2.
. The other angles are shown in Figure 2.
the second triangle is shaded with parallel lines and it represents the triangle of the weight 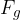 , static component
, static component 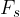 , and the dynamic component
, and the dynamic component 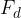 of the weight of the load.
of the weight of the load.
The triangles are similar. We can prove this by looking at Figure 2 and determining the congruence of all the angles.
The first way to determine the components of the weight 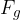 of a body on an inclined plane is to write the ratio of the similar sides of the two similar triangles that represent the geometry of the inclined plane and the weight. In Figure 2, two similar sides of both triangles are drawn with the same colour.
of a body on an inclined plane is to write the ratio of the similar sides of the two similar triangles that represent the geometry of the inclined plane and the weight. In Figure 2, two similar sides of both triangles are drawn with the same colour.
Let's first determine the dynamic component 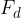 of the weight of the body using the ratio of the lengths of the similar triangles as shown in Figure 2 above:
of the weight of the body using the ratio of the lengths of the similar triangles as shown in Figure 2 above:
Let's also determine the static component 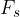 of the weight of the body using the same procedure:
of the weight of the body using the same procedure:
If we know the angle of inclination of the plane, we can calculate the static and dynamic components of the weight of a body on the plane using trigonometric ratios.
Looking at Figure 2, the static component 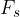 can be expressed using the cosine function:
can be expressed using the cosine function:
The dynamic component 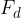 can also be expressed using the sine function:
can also be expressed using the sine function:
At a given angle 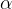 , which represents the inclination of the plane with respect to the horizontal, the static component
, which represents the inclination of the plane with respect to the horizontal, the static component 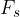 and the dynamic component
and the dynamic component 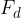 of the weight of a body of mass
of the weight of a body of mass 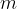 are given as:
are given as:

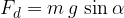
where 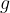 is the gravitational acceleration.
is the gravitational acceleration.
Let's now observe the forces on a body that is at rest or moving on an inclined plane:
In general, the movement of a body on an inclined plane is most often influenced by the following forces:
Dynamic component of the body's weight
The dynamic component of the weight of the body acts through the centre of gravity of the body. This forces the body to move down the plane and its given as:
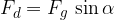
Frictional force
Another force acting on the body on the slope is:
the static frictional force (if the body is at rest) or
the dynamic frictional force (if the body is moving).
Both forces are calculated by multiplying the coefficient of friction 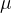 by the normal force
by the normal force 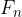 perpendicular to the plane. This force is equal and opposite to the static component
perpendicular to the plane. This force is equal and opposite to the static component 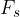 of the weight of the body. The frictional force
of the weight of the body. The frictional force 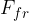 acts in the opposite direction as we push the body. The frictional force acts in the opposite direction to the motion of the body.
acts in the opposite direction as we push the body. The frictional force acts in the opposite direction to the motion of the body.
The static frictional force 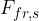 on the plane is therefore given as:
on the plane is therefore given as:
The dynamic frictional force 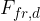 on the plane is given as:
on the plane is given as:
Traction force
In addition to both forces stated above, the body can also be affected by the traction force 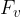 . This can be directed down or up the plane.
. This can be directed down or up the plane.
The dynamic component 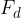 of the weight of the body acts downwards along the plane and is given as:
of the weight of the body acts downwards along the plane and is given as:
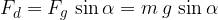
If the body is at rest on the plane, the static frictional force 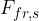 acts on it and it's given as:
acts on it and it's given as:
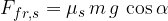
If the body is moving along the plane, the dynamic frictional force 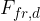 acts on it and it's given as:
acts on it and it's given as:
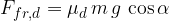
Newton's second law of motion and the Newton's first law of motion also apply on an inclined plane:
A body moves up an inclined plane with uniform acceleration if the sum of all forces acting on it in the direction of the motion is greater than zero.
A body moves uniformly down an inclined plane if the sum of all forces acting on it in the direction of the motion is zero.