A fraction in mathematics represents a rational number and is written in the following form:
where a and b are integers and b is nonzero.
Note: We can also write a fraction as: 
The denominator in the fraction tells us how many equal parts we divide the whole into, and the numerator tells us the number of parts we take.
Let's look at a graphic example of a fractions:
Also, any rational number can be written as a fraction:
Let's look at some special type of fraction. We consider a whole quantity:
The denominator is zero
We know that the whole cannot be divided into 0 equal parts, so the fraction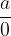 
has no meaning. It follows from the above assumption that the denominator must be non-zero.
The denominator is equal to one
Leaving the whole means that we have divided it into 1 parts. So the whole thing has remained the same and the conclusion follows:
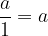
Numerator equals zero
Note that in this case the numerator is zero. This means that 0 is divided into b parts. So each part is equal to 0 and it follows:
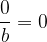
Note: We must take into account the assumption that the denominator is different from 0.
In the following, we will look at the above concepts separately:
The fractions 
and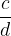 
are the same or equivalent exactly when 
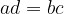. So:
The following applies to the same fractions:
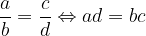
The same fractions are different records for the same rational number.
The set of all rational numbers is denoted by the letter 
. A rational number is a number that can be expressed as the quotient of two integers. This is called fractions. We know that any integer can be written as a fraction with the denominator 1, so rational numbers are extensions of the set of integers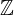 
.
Mathematically, we write this as:
Rational numbers are illustrated on a number line. Each rational number has a specific point on the number line.
A fraction where the numerator is greater than the denominator is always greater than 1, as this means that we took more parts than we got when dividing the whole.
The additive inverse of a fraction is the fraction 
. The sum of the given fraction and its additive inverse must be equal to zero:
Sum of fraction and its corresponding additive inverse:
Note: the additive inverse of the additive inverse of a fraction is equal to the given fraction:
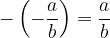
The set of rational numbers is ordered. Exactly one of the following three options applies to the fractions and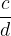 
:
The first fraction is larger than the second:
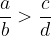
The first fraction is smaller than the second:
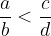
Fractions are identical:
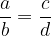
The following properties apply to the relations to be smaller and to be larger:
If we add the same number on both sides of the inequality, the inequality is preserved (sum monotony). If applicable:
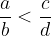
then also applies:
The relation is transitive. If applicable:
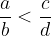
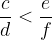
then also applies:
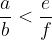
When multiplying an inequality with a positive number, the inequality sign is maintained. If applicable
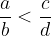
where is:
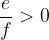
then it also applies
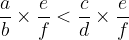
When multiplying an inequality by a negative number, the inequality sign is reversed. If applicable:
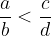
where is
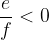
then:
Let us emphasize this point: in the transition to the negative value, the inequality is reversed. So if it is
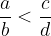
then it follows that it is
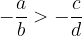
Each rational number can be illustrated as a point on a number line. The image of the larger rational number is on the number line to the right of the image of the smaller rational number.
The images of the image of negative numbers lie to the left of the coordinate origin, and the images of positive rational numbers to the right.
Since the numerator or denominator can also be negative, let’s look at how the sign in the numerator or denominator affects the sign of the whole fraction 
.
Negative numerator
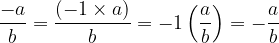
Negative denominator
Negative numerator and negative denominator:
With the help of these statements we can conclude:
If the numerator and denominator have different signs, the fraction is negative, otherwise it is positive.
