If two quantities are interdependent, we can write an expression for them, which we mathematically call a function. The function can be presented in different ways.
Dependent and independent variable
The two quantities may be interdependent; one is called a dependent variable and the other an independent variable:
dependent variable: quantity that depends on another quantity; in mathematics we denote it by y.
independent variable: quantity that can be changed arbitrarily (independently); in mathematics it is denoted by x.
We also say that the dependent variable y is a function of the independent variable x, and we write this with
where f is a rule and f(x) is the value of this function given x.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
A function is a rule that assigns exactly one element from the set B to each element x from the set A. Graphically, this can be illustrated with an arrow diagram.
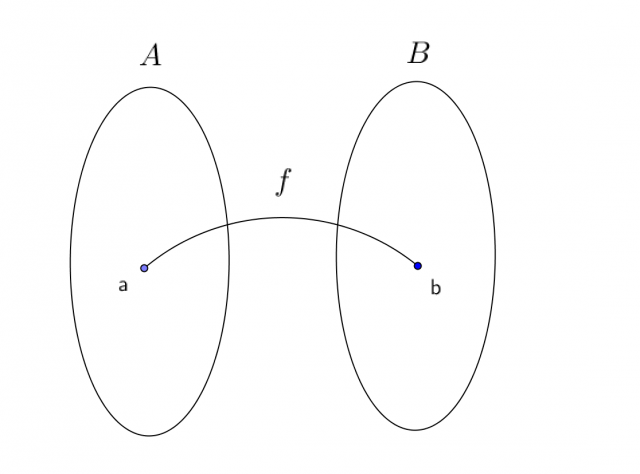
Function  map element a and set A to element b from set B
map element a and set A to element b from set B
We cannot talk about a function when:
rule does not map all elements from the set A
some element from the set A is mapped to two or more elements in the set B
We will agree on the following labeling:
functions are named with the letters:
The statement 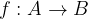 read:
read:
The function f maps elements from the set A to the elements in set B.
The statement 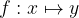 read:
read:
The function f maps element x from set A to element y from set B.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Domain of a function
The Domain 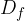 is the set on which the function is defined. The elements are also called the original.
is the set on which the function is defined. The elements are also called the original.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Range
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Presentation of the function
The function can be presented in different ways. Most often we present it with a rule. In case the domain and the range are finite sets, the function can be represented by a table or by an arrow diagram. Real functions can also be represented by a graph.
Function rules
The function can be given by telling how the function maps images. This is stated in the rule:
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Function tabulation
The function can be given with a table in the case where the domain and the range are finite sets. In the first line, enter the values of the independent variable, and in the second, the values of the dependent variable.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
However, if we are talking about a real function of a real variable, the mapping cannot be given entirely with a table. The table can only illustrate some of the values of the function rule.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Arrow diagram
First, we draw two diagrams to illustrate the set A and the set B. We use the arrows to illustrate which elements of the set A are mapped to the elements of the set B.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Function graph
A graph of a function is the basic way to represent a function in mathematics. The graph of the function f is defined as a set of ordered pairs (x, y), where the first element x passes the entire domain of the function, and the second element y is the image of the corresponding x: so the relationship 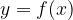 applies between the components. Mathematically, we write this as:
applies between the components. Mathematically, we write this as:
what we read: gamma is the set of all pairs (x, y), where x is the element of the set of the domain 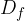 , and y is the mapping of the element x, according to the rule f.
, and y is the mapping of the element x, according to the rule f.
The ordered pairs (x, y) can be drawn in the coordinate system. When the set A is finite (has a finite number of elements), then to each element (x, f (x)) belongs in the coordinate system a point whose abscissa is x, ordinate y so its image is f (x).
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
The x-intercept and the y-intercept
In the following chapters, we will learn to find the the intercepts on the x and y axes.
X-intercept
The x-intercept of a function is the number x for which the value of the function f is equal to 0. The graph of the function intersects the abscissa axis at the value of the variable x for which the function has a value of zero. If we are looking for a computational zero, we find the value xwith the rule:
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Zeros of a polynomial
In the linear equation occurs x to the first power. For this reason, the line is also said to be a first-degree equation; its zero is also called simple zero. The graph of a linear function intersects the abscissa axis at a certain nonzero angle.
In the case of equations of higher powers - these are the equations where the variable x occurs at higher powers (see the chapter polynomial) - we can also talk about the degree of zero. We say that 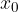 is a zero of degree
is a zero of degree 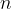 if we can write the equation in the form:
if we can write the equation in the form:
where 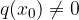 .
.
If n is equal to 2, 4, 6, ... we say that the zero is an even degree. If n is equal to 1, 3, 5, 7 ... we say that the zero is an odd degree.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
In the following we will look at the behavior of the function in odd levels of function.
Even zeros
In even zeros, the graph of the polynomial of the abscissa axis only touches and does not cross it.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Odd Zeros
At zeros of odd degree, the graph of the polynomial fits very well to the abscissa axis and also crosses it.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
y-intercepts
y-intercepts is the point where the graph intersects the ordinate (y) axis. Since the point lies on the ordinate axis, its abscissa is equal to 0, and the ordinate is calculated by inserting 0 for the value x:
The point is therefore of the form: 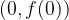 .
.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Injectivity, surjectivity and bijectivity
Injectivity, surjectivity, and bijectivity are properties of a function. Let's take a look at them.
Injective function
The function is injective when it maps different values into different images.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
We check the injectivity in the graph by drawing parallels to the abscissa axis. In the case where the function is injective, each such parallel intersects the graph at only one point. If the line graph intersects at two (or more) points, then the function is not injective.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Surjective function
A function is surjective if its range is equal to the set B. In other words, if each element from the set B is an image to at least one element from the set A.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Bijective function
If a function is injective and surjective at the same time, we say that the function is bijective. In other words, each element from the set B is a picture of exactly one element from the set A.
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »
Example
The example is available to registered users free of charge.
Sign up for free access to the example »
To access the case free of charge, you need to complete your profile.
Finish filling your profile »



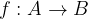 read:
read: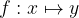 read:
read: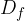 is the set on which the function is defined. The elements are also called the original.
is the set on which the function is defined. The elements are also called the original.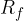 is the set of all
is the set of all 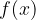 function values. The set
function values. The set 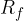 can be the same as the set
can be the same as the set 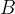 in which the rule is or just a subset of it.
in which the rule is or just a subset of it.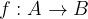

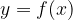
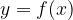 applies between the components. Mathematically, we write this as:
applies between the components. Mathematically, we write this as:
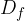 , and y is the mapping of the element x, according to the rule f.
, and y is the mapping of the element x, according to the rule f.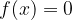
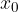 is a zero of degree
is a zero of degree 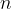 if we can write the equation in the form:
if we can write the equation in the form: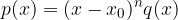
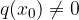 .
.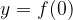
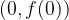 .
.