Personal collections


Combination is a branch of mathematics that deals with counting and explores the number of possible arrangements or selections of given elements.
In the basic theorem of combination, we also encounter a combination tree, which graphically shows us the process of selecting certain elements.
We draw the tree by splitting the nodes forward into as many nodes as we have options in a given step. In the end, when we no longer have the option to choose from, we get the number of all possible combinations.
However, since the tree can become too large, we know different rules for combining combinations in combination.
The basic theorem of combination or the product rule is used when we have at our disposal k successive phases with different number of elements:
in the first phase possible 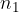 decisions,
decisions,
in the second phase,  decisions are possible,
decisions are possible,
...,
k - this phase, however, 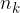 decisions are possible.
decisions are possible.
In doing so, of course, we must take into account that the choices in a particular phase do not depend on the options that were already chosen in previous phases.
If we first choose between 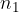 decisions, then independently of the first choice, we choose between
decisions, then independently of the first choice, we choose between  decisions, ... and finally, independently of the previous choice, we choose between
decisions, ... and finally, independently of the previous choice, we choose between 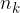 decisions, then the number of all choices (N) is equal to the product of all decisions (
decisions, then the number of all choices (N) is equal to the product of all decisions ( 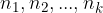 ) in each phase:
) in each phase:
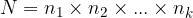
It talks about a situation where we have two or more sets at our disposal that do not have a common cross section, and we choose between the elements of one of all the sets.
The sum rule therefore comes into play when choosing between:
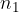 options from the first set of selections
options from the first set of selections
but
 options from another set of selections
options from another set of selections
but
...
but
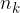 options from another set of selections
options from another set of selections
Selections from each set are incompatible with selections from other sets. We can choose an element from the first or second set, not from both at the same time.
If we choose either one of the 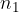 options from the first set or one of the
options from the first set or one of the  options from the second set ... or one of the
options from the second set ... or one of the 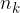 options, we get the number of all selections (M) equal to the sum of the elements (
options, we get the number of all selections (M) equal to the sum of the elements (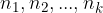 ) from individual sets:
) from individual sets:
