Personal collections


The gas equation shows the relationship among:
pressure,
volume,
temperature
of an ideal gas.
We already learned about the ideal gas in the chapter, Heat and temperature. This is a sufficiently dilute gas where we consider the intermolecular forces to be small enough to be neglected. Gas molecules can be imagined as rigid balls that collide with each other and against the wall of the container. In most cases, an ideal gas is a good enough approximation of a real gas, where the above assumptions are only partially valid.
In addition to pressure, volume, and temperature, in the gas equation, we encounter quantities known to us from chemistry. To make it easier to understand the gas equation, let's briefly discuss those quantities again
The atomic mass unit 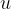 is 1/12 of the mass of the carbon isotope
is 1/12 of the mass of the carbon isotope 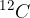 . This is approximately equal to the mass of a hydrogen atom. Its value is given as:
. This is approximately equal to the mass of a hydrogen atom. Its value is given as:
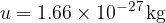
The relative atomic mass 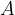 (or molecular mass
(or molecular mass 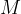 ) tells us how many times the mass of an element (atom or molecule)
) tells us how many times the mass of an element (atom or molecule) 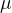 is greater than the atomic unit mass
is greater than the atomic unit mass 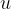 .
.

The relative atomic mass 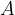 is written in the periodic table of elements next to each element. In the case of a molecule, the relative molecular mass
is written in the periodic table of elements next to each element. In the case of a molecule, the relative molecular mass 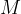 is calculated by adding the relative atomic masses of the atoms that make up the molecule.
is calculated by adding the relative atomic masses of the atoms that make up the molecule.
The mass of a molecule (or atom) 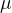 is calculated using the formula:
is calculated using the formula:
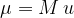
where 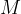 is the relative molecular mass and
is the relative molecular mass and 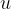 is the atomic mass unit:
is the atomic mass unit:
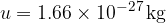
The unit of the quantity of a substance is the mole. One mole of any substance always contains the same number of particles (atoms or molecules), which is given as:
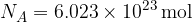
The number 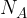 is called Avogadro's number.
is called Avogadro's number.
Instead of the mole, in physics, we usually use the larger unit kilomole ( ). A kilomole of a substance has 1000 times the number of particles in a mole of the substance:
). A kilomole of a substance has 1000 times the number of particles in a mole of the substance:
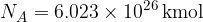
Avogadro's number 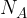 tells us that in one kilomole of (any) substance, the number of particles is always the same and is given as:
tells us that in one kilomole of (any) substance, the number of particles is always the same and is given as:
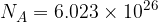
Let's consider it from another angle. A substance is made up of particles. The more particles in the substance, the bigger its quantity. Since a mole tells us how many particles a substance contains, a mole is a unit of the quantity of a substance or a unit that tells us how much of a substance we have
Molar mass is the mass of one mole or the total mass of  particles in a mole of a substance. The unit is
particles in a mole of a substance. The unit is 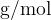 .
.
Since the atoms and molecules of different substances differ in mass, the molar masses of the substances will also be different. The molar mass is determined by the relative atomic mass 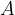 .
.
From the example, we see that the unit 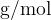 is the same as the unit
is the same as the unit 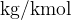 (the numerator and denominator in the unit were multiplied by 1000). In physics, where the basic units are metre, kilogram, and second, we usually also use the unit
(the numerator and denominator in the unit were multiplied by 1000). In physics, where the basic units are metre, kilogram, and second, we usually also use the unit 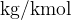 .
.
Difference between molar mass and relative molecular mass.
Although molar mass and relative molecular mass are both denoted by the same letter 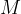 and both have the same numerical value, the concepts differ in unit and meaning.
and both have the same numerical value, the concepts differ in unit and meaning.
Molar mass has the unit 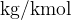 and tells us the mass of one kilomole of a substance - that is, Avogadro's number of particles of the substance.
and tells us the mass of one kilomole of a substance - that is, Avogadro's number of particles of the substance.
Relative molecular mass has no unit. It tells us how many times the atomic mass unit 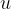 is the mass
is the mass 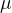 of a particle of a substance:
of a particle of a substance:
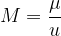
The number of kilomoles of a certain substance is denoted by 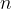 :
:

The unit for mass 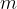 is
is 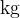 and the unit of molar mass
and the unit of molar mass 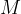 is
is 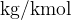 .
.
The number of atoms (or molecules) in the observed mass of a substance is denoted by 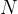 .
.
Since we said in the definition of a mole that 1 mole of a substance has exactly Avogadro's number 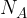 of particles (atoms or molecules), it is therefore considered that
of particles (atoms or molecules), it is therefore considered that 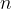 moles have
moles have 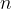 times as many molecules. Therefore, the number
times as many molecules. Therefore, the number 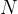 of atoms (or molecules) in an observed mass of a substance is given as:
of atoms (or molecules) in an observed mass of a substance is given as:

When calculating the number of atoms or molecules in an observed substance, we can also simply divide the total mass of the substance 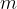 by the mass of a single molecule or atom
by the mass of a single molecule or atom 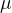 :
:

Before obtaining the final form of the gas equation, partial knowledge was obtained through measurements of how the pressure, volume, and temperature of gases are interdependent. These are Boyle's law and Gay-Lussac's law.
Let's assume we have a certain amount of gas (i.e., a certain number of kilomoles), which we compress or expand, e.g. by means of a piston in a closed cylinder. When the piston is compressed, the volume of the gas decreases and the pressure increases, but their product remains constant. We only have to make sure that the changes are made at a constant temperature - isothermal changes.
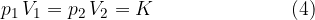
Boyle's law states that at constant temperature, and taking into account the assumption of an ideal gas, the following applies:
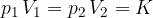
where 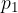 and
and 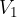 are the initial pressure and volume of the gas before the change,
are the initial pressure and volume of the gas before the change, 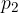 ,
, 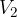 are the final pressure and volume of the gas after the change, and
are the final pressure and volume of the gas after the change, and  is a constant.
is a constant.
Let's draw the graph of  for a kilomole of gas during isothermal changes (
for a kilomole of gas during isothermal changes ( ). We will be able to calculate the constant
). We will be able to calculate the constant 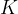 later, but for now, let's just write the value which is given as
later, but for now, let's just write the value which is given as 

Let us take a similar case of a closed cylinder and the same quantity of gas. Now we heat the cylinder. The gas expands with temperature and pushes the piston. The pressure in the vessel remains constant, the changes are called isobaric changes. We notice that the quotient between volume and temperature remains constant:

Charle's law states that at constant pressure, and taking into account the ideal gas assumption, the following applies:
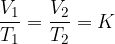
where 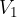 and
and 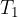 are the initial volume and temperature of the gas before the change while
are the initial volume and temperature of the gas before the change while 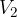 and
and  are the final volume and temperature of the gas after the change, and
are the final volume and temperature of the gas after the change, and 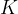 is a constant.
is a constant.
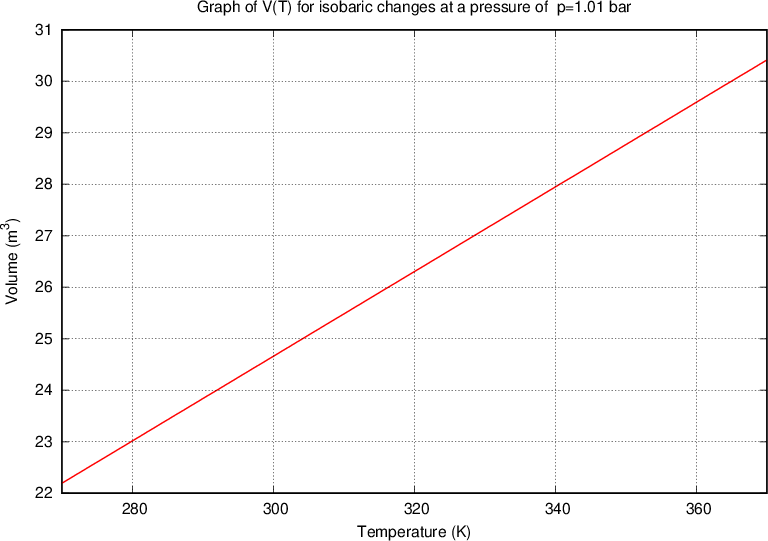
Let's plot the graph of  for isobaric changes (
for isobaric changes (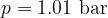 ). We will be able to calculate the constant
). We will be able to calculate the constant 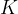 later, but for now, let's write its value for a kilomole of gas and this is given as
later, but for now, let's write its value for a kilomole of gas and this is given as 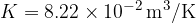 .
.
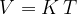
Let's take the example of a closed cylinder with kilomoles of gas. We heat the cylinder with gas. The temperature and pressure of the gas increase, but the volume remains unchanged. Such changes are called isochoric changes. The quotient of pressure 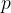 and temperature
and temperature 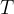 remains constant during heating:
remains constant during heating:

Gay-Lussacs law (or Amontons law or pressure law) states that at constant volume and taking into account the assumption of an ideal gas, the following applies:
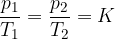
where 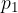 and
and 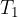 are the initial pressure and temperature of the gas before the change while
are the initial pressure and temperature of the gas before the change while 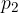 and
and  are the final pressure and temperature of the gas after the change, and
are the final pressure and temperature of the gas after the change, and 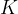 is a constant.
is a constant.
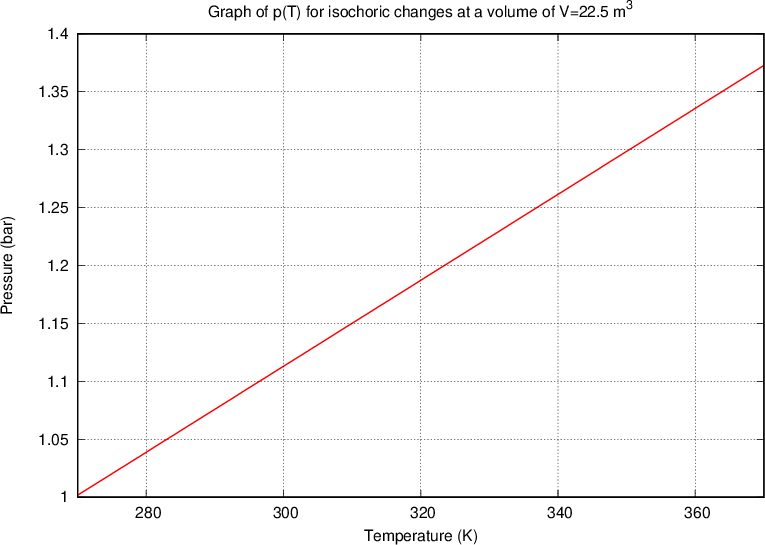
Let's draw the graph of 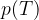 for isochoric changes (
for isochoric changes (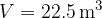 ). We will be able to calculate the constant
). We will be able to calculate the constant 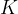 later but for now, let's write the value for a kilomole of gas which is given as
later but for now, let's write the value for a kilomole of gas which is given as 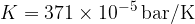 .
.

Let's combine the findings contained in equations 4, 5 and 6:
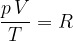
The equation applies to a kilomole of any gas. The constant 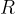 is called the general gas constant and is given as:
is called the general gas constant and is given as:
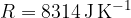
If we have 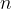 kilomoles of any gas, the gas equation becomes:
kilomoles of any gas, the gas equation becomes:
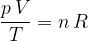
where 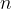 (see equation 2) is given as:
(see equation 2) is given as:
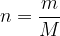
Let's therefore write the gas equation in another form:
The gas equation relates the pressure 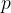 , volume
, volume 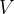 , and temperature
, and temperature 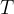 of an ideal gas. It is considered a good enough approximation for real gases as well. Let's note it in two forms:
of an ideal gas. It is considered a good enough approximation for real gases as well. Let's note it in two forms:
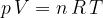
where 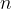 is number of kilomole and
is number of kilomole and 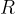 is the general gas constant.
is the general gas constant.
Another form of the gas equation is:
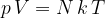
where 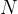 is the number of molecules and
is the number of molecules and 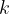 is the Boltzmann constant.
is the Boltzmann constant.
A gas often consists of molecules of different elements, such as air. This consists mainly of nitrogen (78%) and oxygen (21%). Small amounts of carbon dioxide, water vapour, and noble gases (argon) are present in the air.
Let's take a gas, where the number of individual elements is 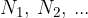 . All elements have the same temperature and are distributed throughout the available volume. Each gas contributes its partial pressure to the total pressure.
. All elements have the same temperature and are distributed throughout the available volume. Each gas contributes its partial pressure to the total pressure.
The pressure of the first element is given as:
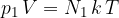
That of the second element is:
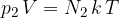
The total gas pressure is equal to the sum of the partial pressures of all the elements:
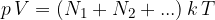
The partial pressures are therefore proportional to the number of molecules but do not depend on the size or mass of the molecule. The written equation is called Dalton's law of partial pressure.
Dalton's law of partial pressure states that the partial pressure of individual molecules or atoms in a gas mixture is proportional to the number of elements in the observed volume and to the temperature.
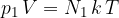
or
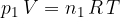
where 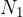 is the number of molecules or
is the number of molecules or 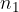 is the number of kilomoles of the given gas element.
is the number of kilomoles of the given gas element.