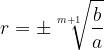A sequence is geometric if the common ratio of two consecutive terms is constant or when each subsequent term of the sequence is calculated by multiplying the previous one by the same number.
We write some consecutive terms of the geometric sequence, denoting the common ratio of two consecutive terms by r, and the first term of the sequence by 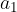 .
.
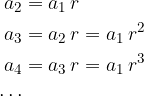
The general term of the geometric sequence:
The formula for the general term of a geometric sequence, where 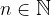 , is:
, is:
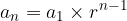
The general term of a geometric sequence is considered to be an exponential function of the variable n.
The ratio of two consecutive terms is called the common ratio of the geometric sequence, denoted by r. The common ratio is always constant.
The formula for the common ratio of a geometric sequence, where 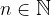 , is:
, is:
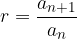
or:
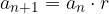
Increasing / decreasing geometric sequence:
The increase and decrease of the geometric sequence depends on the first term 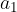 and the common ratio r of the sequence.
and the common ratio r of the sequence.
The variations:
Each term of a geometric sequence, with the exception of the first term, is equal to the geometric mean of the term preceding it and after it.
Geometric mean of any two positive numbers a and b is the number:
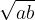
The geometric mean of two arbitrary symmetrically lying terms of a sequence is the term:
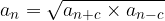
The geometric mean of two positive numbers a and b is less than or equal to the arithmetic mean of the same two numbers:
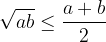
Let's see how we can prove this computationally. We know that the following statement always holds for any numbers a and b:

For the inequality (1), its value will always be positive or equal to 0 only if 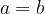 holds.
holds.
Using equation (1), we prove the connection between the geometric and arithmetic mean:
Let's look at graphic proof. We help ourselves with the properties of the angle in a semicircle and the height theorem in a right triangle (see Figure 1).
We draw a semicircle above the line of length a + b and draw two triangles in the semicircle. We can very quickly observe that the arithmetic mean of aand b, 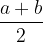 is exactly the radius of the circle, which is at the same time the height of the first triangle.
is exactly the radius of the circle, which is at the same time the height of the first triangle.
What about the height of the second triangle? According to the height theorem in a right triangle, the height to the hypotenuse - the diameter of the semicircle - is equal to 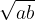 . This is exactly the geometric mean of the numbers a and b.
. This is exactly the geometric mean of the numbers a and b.
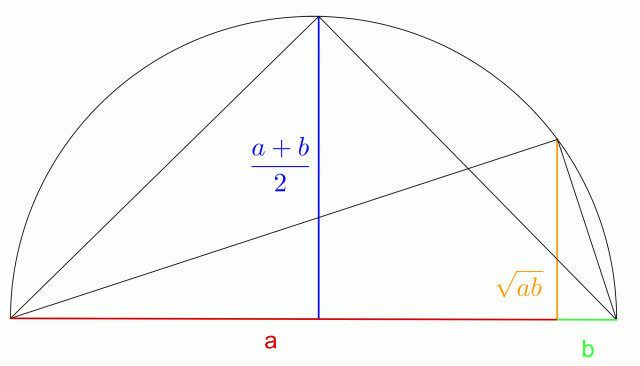
Figure 1: it is obvious that the geometric mean is smaller than the arithmetic one and the same only if the numbers a and b are the same .
Geometric interpolation:
Let us have the numbers a and b and say that we want to insert m numbers between these two numbers so that the numbers 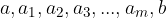 form a finite geometric sequence. This process is called geometric interpolation.
form a finite geometric sequence. This process is called geometric interpolation.
Geometric interpolation gives a geometric sequence that is considered to consist of 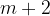 terms, the first term
terms, the first term 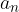 is equal to a and the last term
is equal to a and the last term 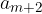 is equal to b.
is equal to b.
Find the formula for calculating the common ratio of a geometric sequence thus obtained:
The formula for the common ratio of geometric sequence, which is obtained by the geometric interpolation procedure when m numbers are inserted between the numbers a and b, is: