A polynomial graph is a continuous curve defined over the entire range of real numbers. When drawing a polynomial graph, it is necessary to know some basic data:
initial value
zero of the polynomials
behavior of the function at infinity
turning points functions
This is the value at which the graph of the polynomial intersects the y-axis. We understand the initial value from a polynomial by looking at a free term:
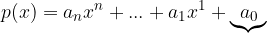
The initial value is the point at which the polynomial has the value of the free term:
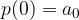
In zeros, the graph of the polynomial crosses or touches the 
axis.
A zero polynomial is a point where the value of the polynomial is equal to 0, so:
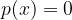
The procedure for finding zeros is explained in more detail in the chapter Finding the zeros of a polynomial. In addition to the zeros themselves, it is also necessary to know the behavior of the polynomial in the area near the zeros; namely, the polynomial can intersect the x axis or just touch it.
When plotting a polynomial graph, we are interested in what is going on around the individual zeros. A polynomial can only touch the abscissa axis at a certain zero, or the graph can cross the abscissa axis and in this case change.
Individual zeros can be single or multi-stage zeros (repeated several times). We recognize two types of zeros:
odd zero
even zero
The degree of zero determines how the graph behaves in their vicinity.
In the vicinity of zero-degree zeros, the graph changes sign and thus crosses the x axis.
In the vicinity of the zeros of the even degree, the graph of the polynomial does not change its sign, since in the zero of the even degree, the polynomial only touches the x axis.
When plotting a polynomial graph, we are also interested in the behavior of the polynomial in infinity. The information we are looking for is whether we start plotting on the positive side of the ordinate axis or on the negative, or whether we end our graph on the positive or negative side. The behavior of a polynomial in infinity depends mainly on the leading term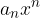 
, and our graph can:
begins at negative values y and ends at positive (increasing)
begins at positive and ends at negative values y (falling)
begins at negative values y and ends at negative (concave)
begins at positive and ends at positive values y (convex)
Let’s look at how the leading term 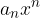affects the behavior of a graph. We are interested in where the graph starts (sign) but not the exact value:
when 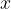goes towards infinity 
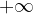, we look at the behavior of the graph on the right.
when 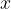goes towards minus infinity 
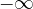, we look at the behavior of the graph on the left.
When the leading term is an odd degree, the sign of the graph is replaced at infinity. If the coefficient is greater than zero, then the graph increases.
When the leading term is an odd degree, the sign of the graph is replaced at infinity. If the coefficient is less than zero, then the graph falls.
When the leading term is an even degree, the sign of the graph is retained. If the coefficient is greater than zero, then the graph starts at positive values and ends at positive values.
When the leading term is an even degree, the sign of the graph is retained. If the coefficient is less than zero, then the graph starts at negative values and ends at negative values.
To understand this chapter, it is necessary to understand the chapter derivation.
Turning point are the points at which a function makes a turn. If we place the tangent to the graph of the polynomial at the extreme, we can see that it is parallel to the axis x.
