

We can draw the basic graph of tangent and cotangent Tangent and cotangent functions.
We will also look at transformations of function graphs:
Extension along the ordinate (y) axis
Extension (contraction) along the abscissa (x) axis
Rigid shift in the direction of the ordinate axis (shift of the function up or down along the y axis)
Rigid shift in the direction of the abscissa axis (shift of the function to the left or right along the x axis)
The value of the angle α is expressed in radians. This means that the value π is equal to 3.14159 ... and not 180°.
The function tan x (or cot x) is multiplied by A, where 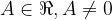 . We get a new feature:
. We get a new feature:

or
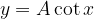
The number A is the amplitude of the function. If
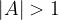 , this means extension of the function in the direction of the axis y;
, this means extension of the function in the direction of the axis y;
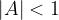 , this means shrinking the function in the direction of the y axis.
, this means shrinking the function in the direction of the y axis.
If A <0, the function is simply mirrored over the abscissa.
When the parameter k is multiplied by x, the extension (or contraction) of the angular function in the direction of the x axis is achieved.
The number k is the frequency of the function, which tells us the number of waves along the length of one period 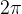 of the function.
of the function.
The higher the frequency, the shorter the period. If
 , the function is stretched in the direction of the x axis;
, the function is stretched in the direction of the x axis;
 , the function shrinks in the direction of the x axis.
, the function shrinks in the direction of the x axis.
The period is the distance made by the function before it starts repeating (the period reflects exactly one round of a unit circle).
The period is most easily imagined on the graphs:
In the first (red) graph we read that the period is  (since at
(since at  the function starts to repeat).
the function starts to repeat).
In the second (green) graph we read that the period is  (since at
(since at  the function starts to repeat).
the function starts to repeat).
In the third (blue) graph, we simply read the period 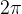 (since at
(since at 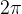 the function starts to repeat).
the function starts to repeat).
Let's conclude:
The period of the function 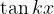 or
or 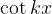 is
is

If:
 , the period is less than
, the period is less than 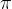
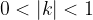 , the period is greater than
, the period is greater than 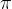
By moving the function in the y axis, we move the function in the coordinate system up (n> 0) or down (n <0).
By moving the function in the direction of the x axis, we move the function in the coordinate system left or right.
The equations are written in the most general possible form

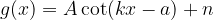
they are written in the most general form. We draw the graphs by combining all the findings of the previous chapters.