Personal collections


Weight or gravity is the force by which masses are attracted. It can work over a long distance. It allows us to stand or walk on the planet Earth, for the Moon to revolve around the Earth, for the Earth and other planets to move around the Sun, etc. Together, it enables the existence of our solar system, our galaxy, and other galaxies.
The cause of gravity is therefore the mass of a body. The masses are attracted. Let's see how we can calculate this attraction and what its consequences are.
The attractive force between two masses can be calculated using Newton's law of gravitation. This says that the force between two masses 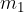 and
and 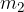 is proportional to the product of the magnitude of the two masses and inversely proportional to the square of the distance
is proportional to the product of the magnitude of the two masses and inversely proportional to the square of the distance  between them:
between them:

where  is the distance between the centres of gravity of the two masses and
is the distance between the centres of gravity of the two masses and  is the gravitational constant which is given as:
is the gravitational constant which is given as:
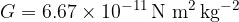
The masses are attracted. The attractive force between two masses is calculated using Newton's law of gravitation:

where  is the distance between the centres of gravity of the two masses, and
is the distance between the centres of gravity of the two masses, and  is the gravitational constant which is given as:
is the gravitational constant which is given as:
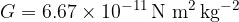
A body of mass  stands on the surface of the Earth. The force acting on the body is called gravity or weight. We learned about it in the material, Force and acceleration and is given as:
stands on the surface of the Earth. The force acting on the body is called gravity or weight. We learned about it in the material, Force and acceleration and is given as:

where 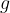 is the acceleration due to gravity. The value of gravitational acceleration decreases with height; on the surface of the Earth, it is given as:
is the acceleration due to gravity. The value of gravitational acceleration decreases with height; on the surface of the Earth, it is given as:
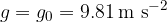
But, how do we calculate it?
Let's review Newton's law of gravitation again:
The gravitational acceleration on the Earth's surface is given as:
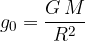
where  is the gravitational constant,
is the gravitational constant, 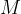 is the mass of the Earth and
is the mass of the Earth and 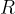 is the radius of the Earth.
is the radius of the Earth.
As we rise from the surface of the Earth, the acceleration due to gravity decreases. Let's draw a sketch!
Let's assume we rise to a height 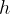 above the surface of the Earth, then our distance
above the surface of the Earth, then our distance  to the centre of the Earth becomes:
to the centre of the Earth becomes:
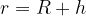
Newton's law of gravitation states that:
We have obtained an equation that determines how the gravitational acceleration changes with height:
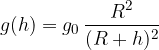
The gravitational force on a body decreases with height and is given as:

Gravitational acceleration 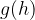 as a function of height
as a function of height 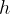 is given as:
is given as:
In the material, Forces in a circular path, we learned that the sum of all forces acting on a body during uniform rotation is equal to the radial force. Here, we assume that the satellite is orbiting at a sufficient height that air resistance is negligible.
A satellite with mass  orbiting at a height
orbiting at a height 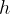 from the Earth's surface is only affected by the gravitational force
from the Earth's surface is only affected by the gravitational force 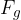 , and this force must be equal to the radial force
, and this force must be equal to the radial force 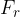 :
:
Gravitational acceleration is equal to radial acceleration. Let's consider: if we want the satellite to orbit the Earth, it cannot be otherwise, because:
if the gravitational acceleration were less than the radial acceleration, the body would escape into space;
if the gravitational acceleration were greater than the radial acceleration, the body would fall to the ground.
The radial acceleration 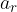 is calculated using any of the available formulas. The one we use depends on the data available to us:
is calculated using any of the available formulas. The one we use depends on the data available to us:

We took into account that the distance from the centre of rotation is 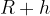 .
.
Even before Newton, the German astronomer Kepler wrote down three laws about the motion of the planets around the Sun. The laws written down after him are called Kepler's laws.
Kepler's first law states that the planets move around the Sun in elliptical paths. The sun is in one of the foci of the ellipse.
In many cases, the foci of the ellipse are close enough to consider the planets moving in a circle. We take the mean distance of the planet from the Sun as the radius.
Kepler's second law states that the connection between a planet and the Sun describes the same areas during its movement along the elliptical path in the same time intervals (see Figure 3).
To make it easier to understand the law, let's draw a sketch:
In Figure 3, we focused on two points:
when the planet is farthest from the Sun. At this point, according to Figure 3, the planet describes an area 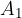 in the time interval
in the time interval 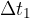 .
.
when the planet is closet to the Sun. At this point, according to Figure 3, the planet describes an area 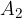 in the time interval
in the time interval 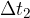 .
.
Kepler's second law states that if the time intervals are equal:

It follows that the described areas are equal:

The law describes the fact that when the planets move closer to the Sun in an elliptical orbit, they move faster. After all, if the two areas are to be the same, the length of the path must be greater than the length of the path at a greater distance in the same observed time.
Kepler arrived at the third law through observation. He found that the quotient of the cube of the planet's distance  from the Sun and the square of its time period of revolution
from the Sun and the square of its time period of revolution 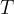 is the same for all planets:
is the same for all planets:
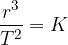
This quotient is called the Kepler constant 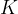 and is given as:
and is given as:
