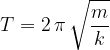Personal collections


The helical spring pendulum consists of a spring and a load attached to the spring. Initially, the load rests in an equilibrium position. When the load is displaced from its equilibrium position and then released, it oscillates around the equilibrium position.
First, let's imagine the load oscillates by sliding without friction on a horizontal surface. In this way, we realise that the force of gravity (weight of the load) is perpendicular to the direction of motion of the pendulum and does not affect the oscillation.
Secondly, let's attach the spring to the load vertically. The force of gravity (weight of the load) now acts in the direction of the pendulum's oscillation. We need to find out if the oscillation frequency will therefore change in any way.
Let's imagine a load of mass 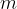 attached horizontally to a spring, slides without friction on a horizontal surface. In the equilibrium position, the spring force is zero. We move the load out of its equilibrium position to the maximum displacement. When moving, we do work: we stretch the spring and give the pendulum elastic energy. Now, let's release the load. All elastic energy is converted into kinetic energy in the equilibrium position. From here, the spring is compressed and the energy is converted back into elastic energy. The process is repeated.
attached horizontally to a spring, slides without friction on a horizontal surface. In the equilibrium position, the spring force is zero. We move the load out of its equilibrium position to the maximum displacement. When moving, we do work: we stretch the spring and give the pendulum elastic energy. Now, let's release the load. All elastic energy is converted into kinetic energy in the equilibrium position. From here, the spring is compressed and the energy is converted back into elastic energy. The process is repeated.
When the pendulum is moved out of the equilibrium position ( ) for the maximum displacement, the spring is tensioned. The spring force
) for the maximum displacement, the spring is tensioned. The spring force  acts in the opposite direction to our motion. It has an inhibitory effect and is therefore negative. We calculate it according to Hooke's law:
acts in the opposite direction to our motion. It has an inhibitory effect and is therefore negative. We calculate it according to Hooke's law:

When the load is released, the force causes acceleration according to Newton's second law:

We note that the acceleration in simple harmonic motion is given as:

Let's insert equations 2 and 3 into equation 1 and get:
The load is attached vertically as shown in the figure below. Will the weight of the load have any effect on the frequency of oscillation due to its vertical position?
Let's look at the figure above. A load (position B) is added to the unstretched spring (position A). Due to the force of gravity (weight of the load), the spring stretches by 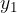 . This is the new equilibrium position. The weight
. This is the new equilibrium position. The weight 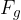 of the load and the force
of the load and the force 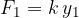 of the spring are in equilibrium at this point.
of the spring are in equilibrium at this point.

With the additional force 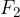 of the hand, we pull the load down by
of the hand, we pull the load down by 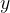 . Now the spring force
. Now the spring force 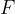 , which acts upwards is:
, which acts upwards is:

The force of gravity 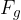 (weight of the load) and an additional force
(weight of the load) and an additional force 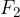 also act downwards. Until we remove our hand, their resultant is equal to zero:
also act downwards. Until we remove our hand, their resultant is equal to zero:
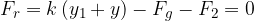
Now, let's release the load (position C). Since now the force of the hand is equal to 0, we get a resultant force 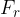 which is given as:
which is given as:
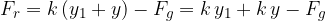
We note from equation 4 above that:
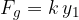
Therefore:
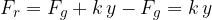
The result is the same as if the load was oscillating horizontally, so the frequency will not change. The pendulum will oscillate as in the first example.
The helical spring has an angular velocity:
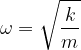
a frequency:

and an oscillation period: