A hyperbola is the set of all points in a plane for which the absolute value is the difference of the distances from the two given points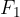 
and 
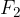constant. The points 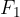and 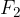are called the foci of the hyperbola.
The geometric definition of hyperbola can be written as:
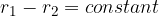
The equation of a hyperbola as a second-order curve is characterized by the fact that the quadratic terms are differently represented:
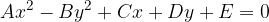
The hyperbola equation will be easier to understand with the help of a sketch, so we first draw a sketch of a typical hyperbola:
The following characteristic elements occur in hyperbola (see sketch):
The foci of the hyperbola are determined by the linear eccentricity e (understood from the sketch):
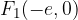
the connection of the linear eccentricity of the hyperbola e with semi major axis a and the semi minor axis b can be deduced from the sketch:
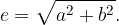
The numerical eccentricity of the hyperbola is:
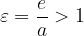
The vertices of the hyperbola are two points (read from the sketch):
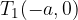
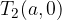
Asymptotes are two intersecting lines to which the branches of the hyperbola approaches. The asymptote equations of the hyperbola are:
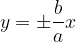
Hyperbola equation in segment form:
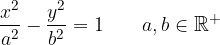
For easier understanding, we draw a sketch of the hyperbola with the real axis on the ordinate axis:
Typical elements of hyperbola are on the ordinate axis:
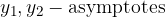
The foci of the hyperbola are determined by the linear eccentricity e (understood from the sketch):
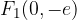
the connection of the linear eccentricity of the hyperbola e with the real pole a and the imaginary pole b can be deduced from the sketch:
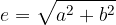
The numerical eccentricity of the hyperbola is:
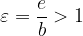
The vertices of the hyperbola are points (understood from the sketch)
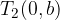
The asymptote equations of the hyperbola are:
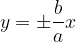
Hyperbola equation in segment form:
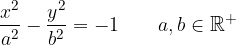
The center of the hyperbola can also be outside the coordinate origin, e.g. at point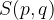 
. we draw a hyperbola with center 
:
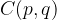The foci of the hyperbola are the points 
and 
, where e is the linear eccentricity of the hyperbola:
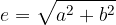
The vertices of the hyperbola are points
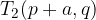
The asymptote equations of the hyperbola are:
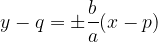
Equation of the hyperbola centered at :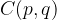
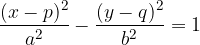
When we look for the intersection between a hyperbola and a line, we solve the system of their equations:
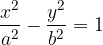
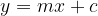
We find the solution by inserting y lines into the hyperbola equation. In general, we have three solutions:
First solution: tangent
A line is a tangent if the system has one double solution:
Second solution: secant
If the system has two different solutions or one solution that is not double is the secant line.
Third solution: no common points
If the system has no real solutions, the line with the hyperbola has no common points.
