Calculating an indefinite integral is the inverse of the derivative operation - we look for the original function from a given derivative. Indefinite integral of the function f (x) is denoted as:
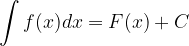
The function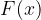 
, which is obtained by integration, is called a primitive function. Since the derivative of the constant is equal to zero, we add any constant to the primitive function C - additive constant.
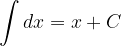
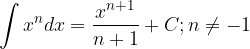
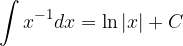
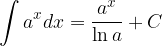
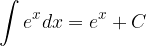
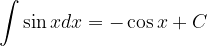
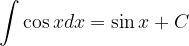
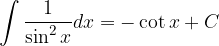
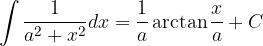
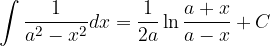
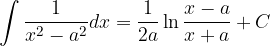
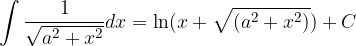
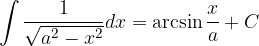
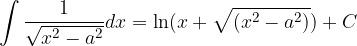
Basic integration rules
Let's look at the basic rules of integration.
The integral of the sum or the difference is equal to the sum or difference of integrals.
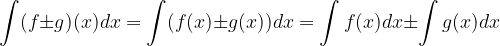
The constant before the function we integrate can be written before the integral sign.
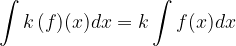
Let us have an integral of the following type:
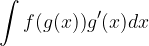
We start integrating by introducing a new variable:
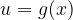
The derivative of the new variable is:
We insert a new variable in our initial integral:
An integral in the form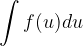 
is often easier to solve than the original notation .
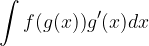The rule is most often used in the integration of the product of an algebraic function (eg quadratic, power, polynomial, root, ... functions) and a transcendent function (eg exponential, logarithmic, trigonometric, ... function) or in the product of two transcendent functions.
Let 
and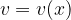 
be derivable functions.
Let's separate their product:
By integrating in parts, we can convert the original integral into a much simpler integral in certain situations. However, we must be careful to choose for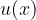 
that part of the integral that is simplified in the derivative.
If we need to integrate the rational function and cannot calculate the integral in one of the ways described above, then we usually try to write such a function as the sum of partial fractions. However, such fractions can be integrated.
