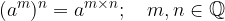Personal collections


Indices with Rational Exponents
We have already learned what the concept, indices, 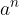 is, where n is a natural number.
is, where n is a natural number.
Fortunately, the same rules apply to indices with rational exponents as well as indices with integer exponents.
Let 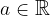 ;
; 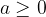 and
and 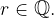 From all fractions that represent a rational number r, choose the one that has the abbreviated numerator and denominator.
From all fractions that represent a rational number r, choose the one that has the abbreviated numerator and denominator.
Let's say this fraction is 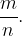 Then:
Then:
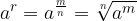
The powers thus defined are calculated in the same way as the powers of whole exponents.
A summary of the rules for calculating powers with a rational exponent (the rules are explained in more detail below) is summarized in the table.
Let 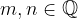 and
and 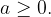 Then apply:
Then apply:
Indices with the same bases are multiplied by picking a base and adding the power exponents:
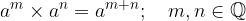
We show this statement by using a different notation of power (with roots) for both powers. Let them be:
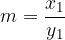
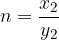
Then the following applies:
When dividing powers of the same bases, we act similarly as when multiplying:
Indices with the same bases are divided by subtracting the exponents:
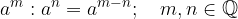
The rules for multiplying and dividing powers by the same exponents are the same as for powers with natural exponents.
Indices with the same exponents and different bases are multiplied by multiplying the bases and taking the common exponent:
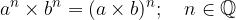
Indices with the same exponents and different bases are divided by dividing the bases and taking the common exponent:
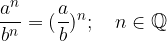
We handle indices with powers by multiplying the power exponents while still retaining the base.
Exponential rule: