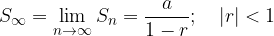Personal collections


An infinite geometric sequence is a special case of an infinite sequence, so let’s get to know an infinite sequence first.
An infinite series is the sum of an infinite number of terms of a sequence of numbers 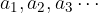 :
:
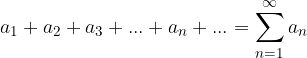
The general (last) term of infinite series is denoted by 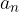 or
or  .
.
An infinite series (which is also called sum) is denoted by the capital Greek letter, 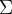 .
.
We write the sums of the first n terms of the sequence:
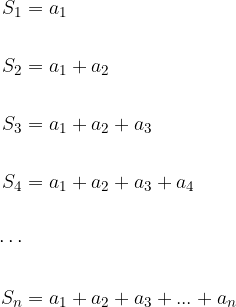
The obtained sums are called partial sums of the sequence. We denote them by  . The sequence
. The sequence  is called the sequence of subtotals.
is called the sequence of subtotals.
The sum of the infinite sequence 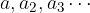 is the limit of the sequence of subtotals when
is the limit of the sequence of subtotals when  . The limit of the sequence of partial sums is denoted by
. The limit of the sequence of partial sums is denoted by 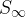 and we write:
and we write:
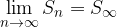
The sum of an infinite series is:
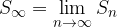
When the limit of the sequence of partial sums exists, we say that the series  converges to the sum
converges to the sum 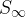 . This means that we can add an infinite number of terms of the sequence.
. This means that we can add an infinite number of terms of the sequence.
However, when the limit of subtotals does not exist or its value is infinite, we say that the series diverges. This means that we cannot add an infinite number of members of the sequence.
Infinite geometric series
Suppose we have a given infinite geometric sequence 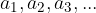 and we want to calculate its sum
and we want to calculate its sum 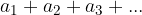 . To calculate the sum of the given sequence, we use an infinite geometric series. Since this is geometric sequence, we know that:
. To calculate the sum of the given sequence, we use an infinite geometric series. Since this is geometric sequence, we know that: 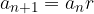 applies, so we can have:
applies, so we can have:
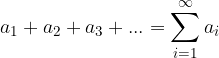
written as:
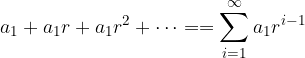
We know that a series is convergent if there is a limit of partial sums, so we find the sum for the first n terms:
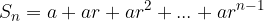
The notation is recognized as a finite geometric series, so it can be written shorter using the form for calculating the sum of the finite geometric series:
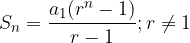
If the series is convergent, then there is a limit to its partial sums, denoted by 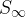 .
.
Let's obtain a formular for 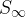 :
:
We note that the limit of the partial sum will exist if the limit of the expression  exist. So, consider when the limit of the expression exist.
exist. So, consider when the limit of the expression exist.
The value of the power 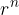 converge towards zero with increasing exponent n if the value of the ratio r is
converge towards zero with increasing exponent n if the value of the ratio r is 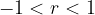 . Therefore:
. Therefore:

For other values of r, the limit of the expression  does not exist.
does not exist.
We conclude that the limit of partial sum exists if:
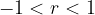
or

We calculate the limit of (1):
The sum of an infinite geometric sequence is as follows: