An infinite limit is a limit that increases beyond all values as our variable approaches the limit value. We write it as:
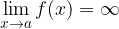
The neighborhood of the point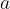 
is the open interval around 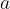centered in 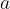. The open interval 
is called the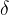 
(delta) neighborhood of the number 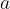. The width of this interval depends on the positive number 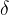, which is usually very small.
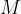is a real value lying on the 
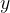-axis. For an infinite limit, it represents the limit beyond which the functional values of 
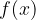grow as 
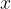approaches the value of .
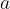The limit is infinite if for any value of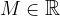 
that we can find such 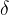that when x in 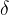- around the point a, i.e. 
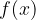, will be greater than .
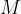Limit
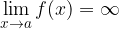
is infinite if for every 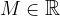there exists a 
that holds: if
then follows
Example of an infinite limit
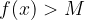
Using the limit, we can determine the course of the vertical asymptote in the graph. If so
then the graph of the function 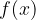has a vertical asymptote in 
.
Let's have the function 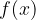. If applicable:
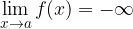
then the following applies equally:
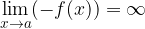
Let's illustrate graphically (the graphs are symmetrical with respect to the abscissa axis):
Function has a negative infinite limit
Function 
has a positive infinite limit
