Personal collections


An infinite limit is a limit that increases beyond all values as our variable approaches the limit value. We write it as:
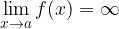
The neighborhood of the point 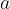 is the open interval around
is the open interval around 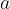 centered in
centered in 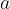 . The open interval
. The open interval 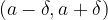 is called the
is called the 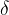 (delta) neighborhood of the number
(delta) neighborhood of the number 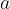 . The width of this interval depends on the positive number
. The width of this interval depends on the positive number 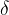 , which is usually very small.
, which is usually very small.
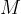 is a real value lying on the
is a real value lying on the 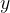 -axis. For an infinite limit, it represents the limit beyond which the functional values of
-axis. For an infinite limit, it represents the limit beyond which the functional values of 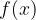 grow as
grow as 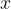 approaches the value of
approaches the value of 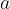 .
.
The limit is infinite if for any value of 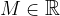 that we can find such
that we can find such 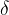 that when x in
that when x in 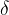 - around the point a, i.e.
- around the point a, i.e. 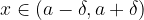 ,
, 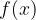 will be greater than
will be greater than 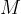 .
.
Limit
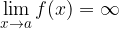
is infinite if for every 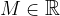 there exists a
there exists a 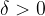 that holds: if
that holds: if
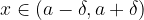
then follows
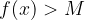
Using the limit, we can determine the course of the vertical asymptote in the graph. If so
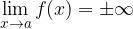
then the graph of the function 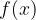 has a vertical asymptote in
has a vertical asymptote in 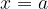 .
.
Let's have the function 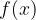 . If applicable:
. If applicable:
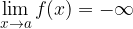
then the following applies equally:
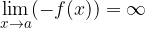
Let's illustrate graphically (the graphs are symmetrical with respect to the abscissa axis):