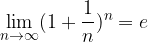The sequence is infinite if it does not have the last term or its terms continue indefinitely. In mathematics, infinite sequences are common, many of which we have known for a long time: a sequence of natural numbers, a sequence of even / odd numbers, a sequence of squares of natural numbers, and so on.
Sequences can be infinite, but still limited by a certain limit or the sequence terms approach the same number. In this chapter, we will look at how to recognize such a sequence and write down its properties.
We can often observe that an infinite number of terms of any sequence lie around a certain point. We say that such an infinite sequence is finite, and that for it there exists some such real number to which the values of its terms approach. Before we take a closer look at the existence and properties of this real number, let's first get to know the neighborhood of (some) point.
We met the neighborhood of the point already at the limit of the function, where we realized that:
The neighborhood of any point a is the open interval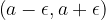 
.
- point vicinity a
The neighborhood of the point is called 
- the neighborhood of the point a and is marked with the code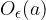 
. The number a is the centre of the neighborhood, and the positive number is called the radius of the neighborhood.
We learned one of three ways we can write - the neighborhood of point a. Let's meet the other two.
- the neighborhood of point a can, in addition to the notation with an interval, be written in two other ways:
as a composite inequality: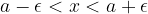 
,
as absolute value: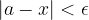 
We know that the vicinity of a point is an arbitrarily wide open interval, its width or the width around the point depends on the value of the number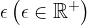 
. Usually for we take a very small number, especially when we want to prove something.
Width - neighborhood is the width interval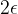 
.
In sequences, we often observe that many of its terms lie around a certain point. Let's take a closer look at such a sequence.
We take a sequence with the general term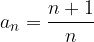 
and write down some of its terms:
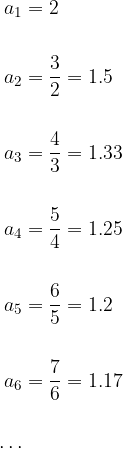
Apparently the given sequence is bounded upwards, where its upper limit is equal to the first term of the sequence,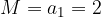 
.
If we continue to write the terms of the given sequence, we notice that the terms of the given sequence approach the number 1:
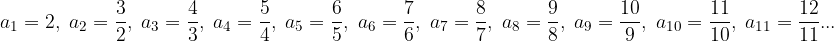
We observe the neighborhood of the number 1, whose half width is equal to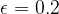 
(see Figure 1, red). Apparently the fifth term 
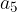is still outside the 
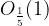neighborhood, while the sixth term is 
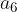, and all the others that follow it are already inside that same neighborhood.
We also observe the surroundings of the number 1 at 
(see Figure 1, green). Apparently this time the tenth term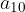 
is outside the neighborhood 
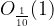, the eleventh term 
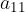, and all the others that follow it are already inside the - neighborhood.
Figure1
Let's check our observations with a calculation. Is it really true that 
and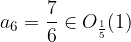 
?
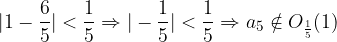
Let's also check for the surroundings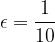 
. Does 
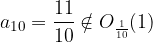and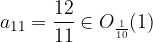 
really apply?
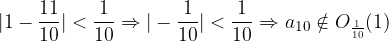
We conclude that no matter how many times we reduce the neighborhood of the number 1, there is always some such value of the variable N, which is considered to be infinitely many terms of the sequence in - the neighborhood of the number 1, and outside this neighborhood only finally a lot. In other words, outside - the environs of number 1 can only lie a finite number of terms of the sequence.
In a given sequence 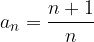, these properties apply to the number 1, so the number 1 is called the sequence limit.
Write down the definition of sequence limits.
The number a is the limit of the infinite sequence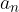 
, if for every even small positive number there exists such a natural number N that for every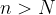 
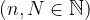the following holds:
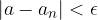
Write the limit of an infinite sequence as follows:
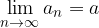
So, in a given sequence , we would write the limit of the sequence as:
If a sequence has a limit, we say that the sequence converges and we call it a convergent sequence.
Each increasing and upward-bounded sequence is convergent (has a limit). The same applies to the decreasing and downward bounded sequence.
A typical example of a convergent sequence is constant sequence, as it is obvious that in any - constant environment, all terms of the sequence are always located.
It is also considered that every geometric sequence with a common ratio of 
is a convergent sequence.
A sequence that is not convergent and has no limits is called a divergent sequence.
Any arithmetic sequence 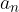with a common difference other than zero, 
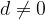, is a divergent sequence.
Any geometric sequence 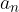with common ratio equal to - 1, 
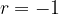is a divergent and alternating sequence.
Any geometric sequence 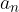with common ratio 
is a divergent sequence.
Let's take a closer look at one of the sequences from the example above with the general term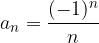 
:
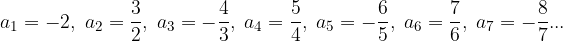
Let's illustrate the sequence on the number line:
Figure 2
We see that the terms of the sequence approach two different numbers, the numbers 1 and -1, which are NOT the limits of the sequence. How come?
A number of a sequence limit is considered to be if, from a certain term onwards, ALL terms of the sequence lie within an arbitrarily small neighborhood of that number (limits).
Take any small neighborhood of the number -1 (see Figure 2, green). We can see from the picture that the fifth link of the sequence lies inside the surroundings, while the next link, the sixth link, already lies outside the surroundings. Obviously the definition for a limit does not apply to the number -1 and therefore the number is not really the limit of the sequence.
Take any neighborhood of the number 1 (see Figure 2, green). Again, we can see from the picture that the sixth term is part of the neighborhood of the number, and the seventh term already lies outside the neighborhood. Obviously, the number 1 is not the limit of the sequence either.
As we concluded in the previous example, a given infinite sequence is divergent and without a limit, but it has two intersections, namely the numbers 1 and -1.
The intersection of a sequence is the number a, which has in any - neighborhood of a point, infinitely many members of a given sequence.
We know that:
The sequence limit is also the intersection of the sequence, and vice versa is generally not valid.
and:
A finite infinite sequence has at least one intersection (Weierstrass theorem).
also:
If a sequence has multiple intersections, then it certainly has no limits.
The following rules apply to computation with convergence sequence limits:
Constant limit is:
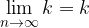
Sequence limit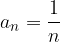 
is equal to 0:
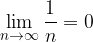
The sum of a limit is equal to the limit of a sum:
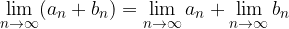
The difference of a limit is equal to the limit of the differences:
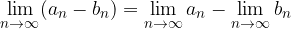
The product limit of the constant and sequence is equal to the sequence limits multiplied by the constant:
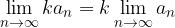
The product limit is equal to the product of each limit:
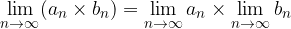
The quotient limit is equal to the quotient limit if the divisor limit is different from zero and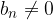 
applies to each natural number:
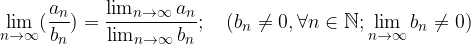
The geometric sequence limit 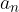with common ratio 
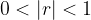is equal to 0 for each natural number:
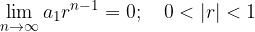
The limit of the nth root of the sequence is equal to 0 for each term greater than 0:
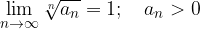
We also connect an irrational number e with infinite sequence and limits, called Euler's number after the Swiss mathematician, physicist and astronomer Leonhard Euler.
The number e is already known from the chapter Logarithm, where we recognized it as the basis for the natural logarithm, and found that its approximate value is equal to 
.
Euler's number e can be expressed by a limit:
