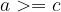To put it simple, integers are just extended natural numbers, the set of natural numbers, add 0 and negative natural numbers. The set of integers is denoted by:
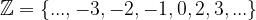
but
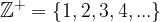
which is exactly 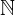 , while
, while
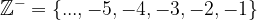
and we see that it is 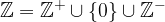 and we say that the set of natural numbers consists of the set of positive integers (which is the set of natural integers), the set of negative integers, and the number zero.
and we say that the set of natural numbers consists of the set of positive integers (which is the set of natural integers), the set of negative integers, and the number zero.
Since integers are just extended natural numbers, they can be represented on number line. We extend it by mirroring all natural numbers over the starting point - making all integers to the left of the starting point negative.
Extend the line with natural numbers to the left:
A unit to the left, we get 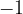
One unit to the left of 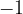 , we get
, we get 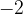
We repeat the process by applying the unit evenly to the left to obtain the remaining negative numbers.
The number 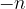 is called the additive inverse of
is called the additive inverse of 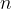 . Natural numbers are positive integers, and mirrored natural numbers are additive inverse.
. Natural numbers are positive integers, and mirrored natural numbers are additive inverse.
Addition and multiplication of integers are defined similarly to addition and multiplication of natural numbers. In addition to these two basic arithmetic operations, we also define subtraction in the set of integers.
The subtraction is defined as the addition of the additive inverse: 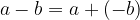 , where
, where 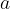 is called the minuend,
is called the minuend, 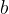 is the subtrahend and the result of
is the subtrahend and the result of 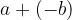 is the difference.
is the difference.
For integers, in addition to properties of arithmetic operations natural numbers, some rules also apply.
When adding 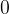 to any integer, the result does not change.
to any integer, the result does not change.
Identity element:
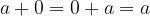
for each  of
of 
The sum of any integer and its additive inverse equal 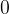 .
.
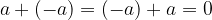
The additive inverse of 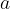 is
is 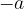 .
.
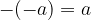
The negation of a sum is equal to the sum of its additive inverses.
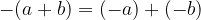
The number 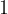 is the multiplication identity element.
is the multiplication identity element.
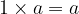
Multiplying 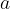 by
by 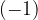 gives the additive inverse of the number
gives the additive inverse of the number 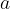 .
.
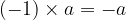
When multiplying any number by 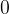 , the result is always equal to
, the result is always equal to 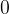 .
.
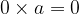
The product of two negative integers is positive.
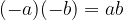
The product of two positive integers is positive.
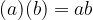
The product of a negative and a positive is negative.
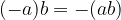
When calculating, we follow the order of arithmetic operations (multiplication takes precedence over addition and subtraction), and in the case of brackets, we always eliminate these first. In doing so, we must pay attention to the signs:
If the brackets are preceded by a plus sign (+), the numbers in the brackets retain their sign:
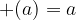
and
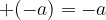
If the brackets are preceded by a minus sign (-), the numbers in brackets change their sign:
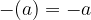
and
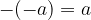
In a set of integers, we can compare any two numbers with each other and determine whether they are the same (=) or which of them is greater (>) or less (<). The inequalities less than or equal to (<=) or greater than or equal to (> =) can also apply.
For any integers 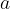 and
and 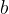 ,
, 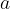 is greater than
is greater than 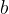 , which is written with symbols:
, which is written with symbols:
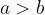
if and only if
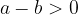
or if 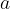 lies to the right of
lies to the right of 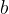 on the number line.
on the number line.
For any integers 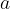 and
and 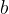 ,
, 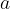 is less than
is less than 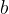 , which is written with symbols:
, which is written with symbols:
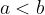
if and only if
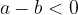
or if 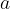 lies on the left side of
lies on the left side of 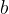 on the number line.
on the number line.
For any integers 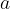 and
and 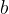 ,
, 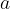 is equal to
is equal to 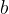 , which is written with symbols:
, which is written with symbols:
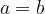
if and only if
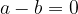
or if 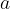 coincides with
coincides with 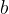 on the number line.
on the number line.
For any integers 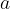 and
and 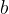 ,
, 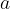 is less than or equal to
is less than or equal to 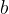 , which is written with symbols:
, which is written with symbols:
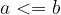
if and only if
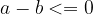
or if 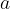 lies on the left side of
lies on the left side of 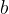 or coincides with it on the number line.
or coincides with it on the number line.
For any integers 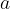 and
and 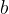 ,
, 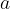 is greater than or equal to
is greater than or equal to 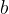 , which is written with symbols:
, which is written with symbols:
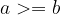
if and only if
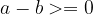
or if 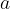 lies on the right side of
lies on the right side of 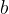 or coincides with it on the number line.
or coincides with it on the number line.
If we add the same number on both sides of the inequality, the inequality is maintained:
if
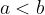
then it is true for
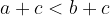
"Less than" is transitive:
if 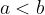 and
and 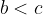 , then
, then 
When multiplying inequalities by a positive number, the inequality sign is retained:
if 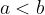 and
and 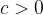 then
then 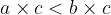
When multiplying inequality by a negative number, the inequality sign is reversed:
if 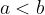 and
and 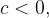 then
then 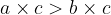
"Less than or equal to" is reflexive:
if 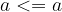
"Less than or equal to" is antisymmetric:
if 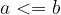 and
and 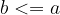 , then
, then 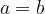
"Less than or equal to" is transitive:
if 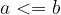 and
and 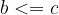 , then
, then 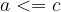
"Greater than or equal to" is reflexive:
if 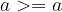
"Greater than or equal to" is antisymmetric:
if 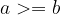 and
and 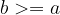 , then
, then 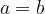
"Greater than or equal to" is transitive:
if 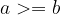 and
and 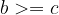 , then
, then