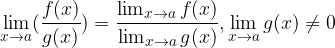The neighbourhood of the point 
on the number line is an open interval centred in .
Neighbourhood
If the boundaries of the interval are distant from the point by 
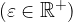, then we write this interval of width 
: 
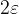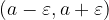and call it the - neighbourhood of the point . Let's mark it:
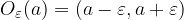
The neighbourhood can be an arbitrarily large interval, the width of the interval depends on the choice of a positive number (which, however, is usually very small when we want to prove an assertion).
The number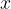 
is in - neighbourhood of if it is less than 
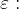from
The neighbourhood of the point can therefore be written as the set of all such real numbers 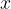, which are less than 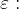away from
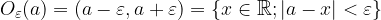
When does the 
function limit exist at a given point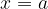 
?
We choose any small positive real number that determines the neighbourhood of the point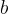 
on the ordinate axis. Check that there is such a positive real number 
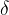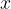for the selected that all values of from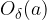 
on the abscissa axis (except perhaps the point ) are mapped to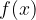 
from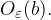 
If it exists, then we say that the limit of the function at point exists and is equal to 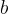. It does not matter whether the function is defined in point or not.
Function at is defined. There is a limit.
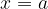The function at is not defined. There is a limit.
, if for each 
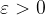there exists a 
that is valid:
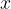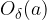if is in and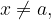 
is also 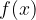in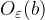 
.
Or:
Limit
exists if for each 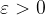there exists a such that:
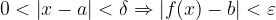
When defining the limit of a function, it is important that for every small we can find a corresponding 
, otherwise there is no limit at the point .
The following rules apply to calculating limits (if, of course, there are limits for individual functions at ):
1. The sum limit is equal to the sum limit of individual function:
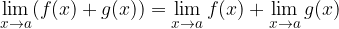
2. The limit of the product of the constant factor and the function is equal to the limits of the function multiplied by the constant:
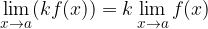
3. The product of a limit is equal to the product of individual limit:
4. The limit of the quotient is equal to the limit of individual function of the quotient if the limit in the denominator is not equal to zero:
