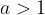The limit at infinity describes the behavior of functions and their graphs far away from the coordinate origin when the independent variable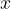 
grows across all boundaries in the positive or negative direction.
We write it as:
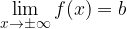
Let's have the following definition:
The neighborhood of a point:
The neighborhood of the point 
is the open interval around centered at . The open interval 
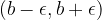is called the 
(epsilon) neighborhood of the number . The width of this interval depends on the positive number , which is usually very small.
The value M:
The value of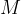 
is the real value lying on the 
-axis. For the limit to infinity, it represents the limit beyond which all functional values of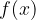 
lie in the neighborhood of when approaches the value at infinity.
The limit in infinity is located at point when goes to infinity, if for each selected 
we find such a real number 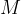such that for all greater than 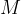are mapped the - neighborhood of the point .
SO,
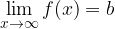
if for each 
there exists a real number 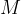such that:
if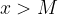 
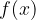, is in the - neighborhood of the point .
Example of limit at infinity
Let's have the function 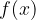. If:
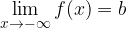
then the following applies:
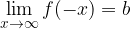
The limit to infinity for mirror graphs (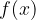 and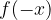 
are symmetric with respect to the y - axis) the following applies:
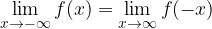
We will focus on rational functions where the degree of the polynomial at the numerator is a maximum of 1 greater than the degree of the polynomial at the denominator. We set this condition because we want to limit ourselves to the most linear asymptotes.
The following applies:
The graph of the function approaches the abscissa axis far away from the coordinate origin.
It follows that:
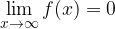
The following applies:
The graph of the function approaches the horizontal asymptote with the function far away from the coordinate origin:
where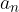 
and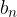 
are the leading coefficients of these two polynomials.
It follows:
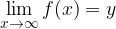
The following applies:
The values of such a rational function grow beyond all limits when goes to infinity. The graph approaches the oblique asymptote.
It is also true that the larger the value, the smaller the distance between the function and the oblique asymptote. Which means that the larger the , the smaller the difference between the value of the rational function and the value of the linear function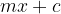 
, i.e. the quotient of the numerator and denominator.
The value 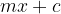represents the equation of the oblique asymptote, which is obtained as follows:
Let us have a rational function of the form:
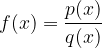
To calculate the oblique asymptote, we must divide the polynomial in the numerator - 
by the polynomial in the denominator -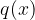 
. We get:
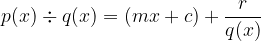
For the remainder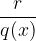 
we know that the larger , the smaller this term. So when goes to infinity it goes against nothing.
It follows that the equation of the oblique asymptote is:
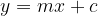
As the independent variable increases, the difference between the value of the function 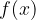and the quotient 
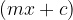becomes smaller, so it limits to zero:
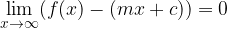
Let's recall the form of the exponential function:
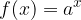
We know that the limit at infinity in a value a exists only when the function approaches this value a as the value x increases, so we must pay attention to the sign of infinity to which we 'send' x. It follows that the above statement applies only in cases where one of the following conditions is met:
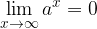
if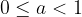 
or
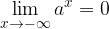
if 
