Personal collections


Logarithmic equations are equations in which the unknown occurs in the logarithm or in the base of the logarithm. We encounter a logarithmic equation when we want to calculate the intersection of a graph of a logarithmic function with any other function (linear, quadratic, exponential ...)
We distinguish logarithmic equations according to the procedure by which we solve them.
At the end of the solution, we always do a test, because in the initial equation the logarithm and the base must be positive real numbers and the base must be different from 1.
Logarithmization solves equations of the type:
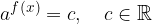
The equation can be logarithmic with the logarithm of any bases. If possible, the base of the logarithm should be equal to the base of the power. We usually have logarithm with the base 10 or the base e, because we have these two logarithms on a pocket computer and this is the easiest way to calculate the approximation of the solution.
We solve simple logarithmic equations with the definition:
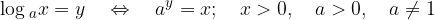
In solving the following logarithmic equations, we will use logarithmic rules
If several logarithms with different bases appear in the equation, the equation is first transformed into such a form that all logarithms have the same bases. For the new base, we choose the smallest of the given bases.
By introducing a new unknown, we solve higher-level logarithmic equations and equations in which the logarithm appears in the form of an algebraic fraction. The new equation is more transparent and easier to solve.
When a logarithmic equation cannot be solved by any of the methods already written, we solve it graphically. We rearrange the equation we are solving so that the functions we know how to draw appear on both sides. This is followed by drawing both functions in the same coordinate system. The solutions of our equation are the x axis of the points at which the graphs intersect. The solution is confirmed by an arithmetic test.
Logarithmic inequalities are inequalities in which the unknown appears in the equation of the logarithm. We usually solve the inequalities graphically, which means that we draw both graphs that appear in the inequality. Simpler inequalities can also be solved by calculation.